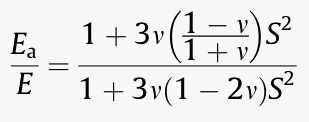Compression of a block
 The Young's modulus E of a material can be determined via a tension or compression experiment upon a slender bar of material, provided the lateral surfaces are free of stress. For a thick bar or block, the lateral deformation associated with Poisson's ratio is restrained by frictional contact with the compression surfaces of the test device. The specimen bulges and the modulus measured differs from the true Young's modulus The effect has been calculated via approximate methods by several authors.
The Young's modulus E of a material can be determined via a tension or compression experiment upon a slender bar of material, provided the lateral surfaces are free of stress. For a thick bar or block, the lateral deformation associated with Poisson's ratio is restrained by frictional contact with the compression surfaces of the test device. The specimen bulges and the modulus measured differs from the true Young's modulus The effect has been calculated via approximate methods by several authors.
The apparent Young's modulus Eapp of a compressed rubber cylindrical block is given by [1], with a as radius and h as thickness.
Eapp = E ( 1 + 2 s2 ) = E ( 1 + a2 / 2 h2)
in which E is the true Young's modulus and s is the ratio of one loaded area to the force-free area.
Similarly, for a rectangular block of square cross section,
Eapp = E ( 1 + 2.2 s2 )
Rubber has a Poisson's ratio approaching 1/2. If the Poisson's ratio has another value, the correction formula differs. The general relations are rather complex [2]. Some special cases are given for Poisson's ratio from 0 to 1/3 [3]. For a cylinder with diameter equal to its length and Poisson's ratio of 0.3, then
Eapp = 1.03 E.
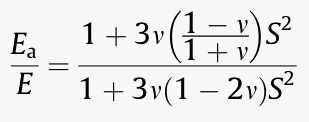
For any Poisson's ratio, results for a cylinder [4] are given above. Here S = a/h, the ratio of radius to height.
References
1 A. N. Gent, P. B. Lindley, "The compression of bonded rubber blocks", Proc Instn Mech Engrs, 173, 111-117, (1959).
2. L. N. G. Filon, "On the equilibrium of circular cylinders under certain practical systems of load", Philosophical Trans. Royal Society of London, England, Ser. A, 198, 147-233 (1902).
3. K. T. Chau, "Young's modulus interpreted from compression tests with end friction", Journal of Engineering Mechanics, ASCE, 123, 1-7, (1997).
4. J.G. Williams, C. Gamonpilas, "Using the simple compression test to determine Young's modulus, Poisson's ratio and the Coulomb friction coefficient" International Journal of Solids and Structures 45, 4448-4459 (2008).
Top
 The Young's modulus E of a material can be determined via a tension or compression experiment upon a slender bar of material, provided the lateral surfaces are free of stress. For a thick bar or block, the lateral deformation associated with Poisson's ratio is restrained by frictional contact with the compression surfaces of the test device. The specimen bulges and the modulus measured differs from the true Young's modulus The effect has been calculated via approximate methods by several authors.
The Young's modulus E of a material can be determined via a tension or compression experiment upon a slender bar of material, provided the lateral surfaces are free of stress. For a thick bar or block, the lateral deformation associated with Poisson's ratio is restrained by frictional contact with the compression surfaces of the test device. The specimen bulges and the modulus measured differs from the true Young's modulus The effect has been calculated via approximate methods by several authors.