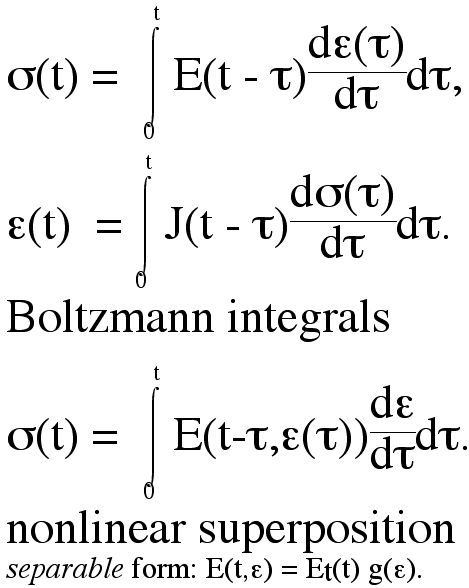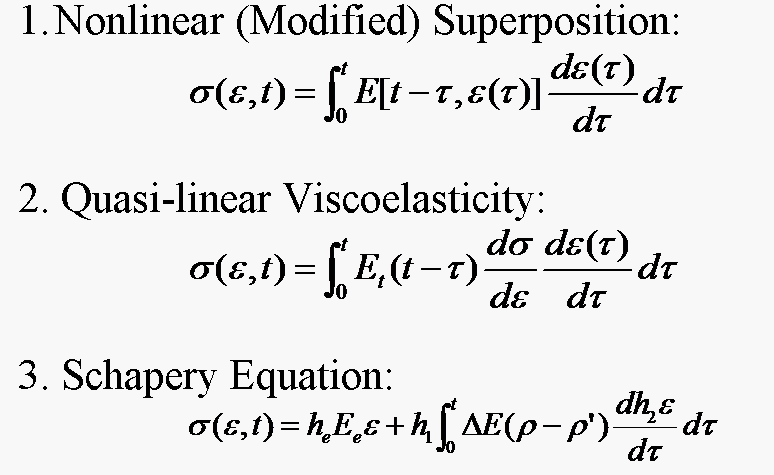How to characterize nonlinear viscoelastic solids
Characterization of nonlinear viscoelastic solids
Do a series of creep experiments at different stress or relaxation experiments at constant strain.
Plot creep compliance J versus time t and stress or relaxation modulus E versus time t and strain. The test will be most definitive if the largest possible window in strain and in log time is used. To attain a wide time window, the rise time of the imposed step in strain should be as short as possible. A slow ramp is not helpful in this regard.
If the creep compliance curves corresponding to different stresses (or the relaxation modulus curves corresponding to different strains) overlap, the material is linearly viscoelastic. Creep compliance is independent of stress and relaxation modulus is independent of strain.
In a plot of log compliance vs. log time, if the curves are separate but have the same shape, then the behavior is consistent with quasilinear viscoelasticity (QLV), a model originally after Y. C. Fung. QLV assumes the creep compliance can be written as a product of a function of time and a function of stress. If the compliance is in fact a product, then all the creep curves have the same shape (the same functional form).
Suppose one generates a stress-strain curve at constant strain rate, as well as a single creep test or a single relaxation test. If the stress-strain curve has a concave up nonlinearity, then the material is nonlinear. If the creep or relaxation test reveals time dependence, then the material is viscoelastic. It might obey QLV or it might obey nonlinear superposition, but the test is not definitive either way. One cannot make a correct inference about the type of viscoelastic model from such an experimental protocol.
If the curves for creep at different stress have different shape (or slope in a double log plot), then neither linear viscoelasticity nor QLV describe the behavior, because the relaxation modulus function depends on both time and strain, and the creep compliance function depends on both time and stress. The material may obey a more general nonlinear superposition law such as nonlinear superposition in which the relaxation modulus function is written explicitly as a general function of time and strain.
To do this test properly a sufficiently wide window of load level is required to discriminate he slopes of the different curves. Similarly, a sufficiently wide window of time is required to properly delineate the slope of each curve.
For example, the following results show ligament is nonlinearly viscoelastic but does not obey QLV, because QLV predicts the same slope independent of strain. To display nonlinearity, plot the ratio of stress to strain versus time.

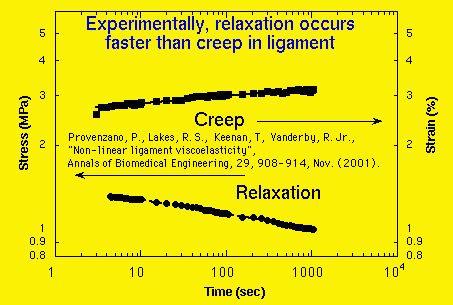
One can also conduct separate creep and stress relaxation tests on the same material. For linear materials, creep and relaxation are related by a convolution. If creep follows a power law, so does relaxation, with the same slope. For nonlinear materials, if creep follows QLV, then relaxation will not obey QLV but will be more generally nonlinear. For example, the following results show ligament is nonlinearly viscoelastic since the slope differs. The difference in slope also shows it does not obey QLV.
In a recovery experiment, the strain is set to zero after a period of relaxation or the stress is set to zero after a period of creep. In both a linearly viscoelastic solid and one which follows QLV, recovery must initially follow the same dependence as the creep or relaxation which preceded it. For nonlinear superposition, or for a material describable by a Schapery model recovery can have a different time dependence.
Several constitutive equations are shown below. Boltzmann integrals refer to linear viscoelasticity. If the strain follows a step in time, the stress follows the modulus kernel function within the integral. A subsequent step down in strain gives rise to recovery, and allows comparison between models. Other nonlinear constitutive equations are known for viscoelastic materials; some involve multiple integrals.
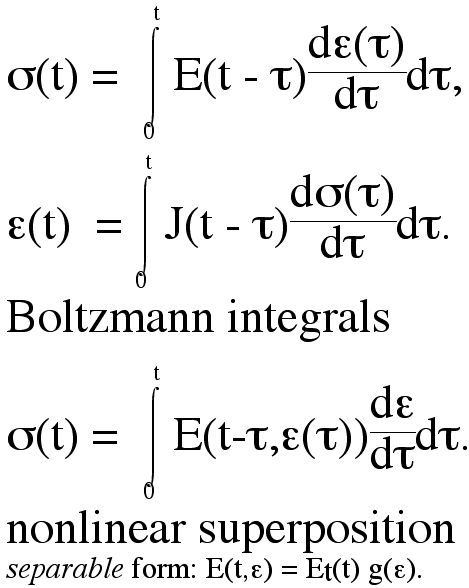
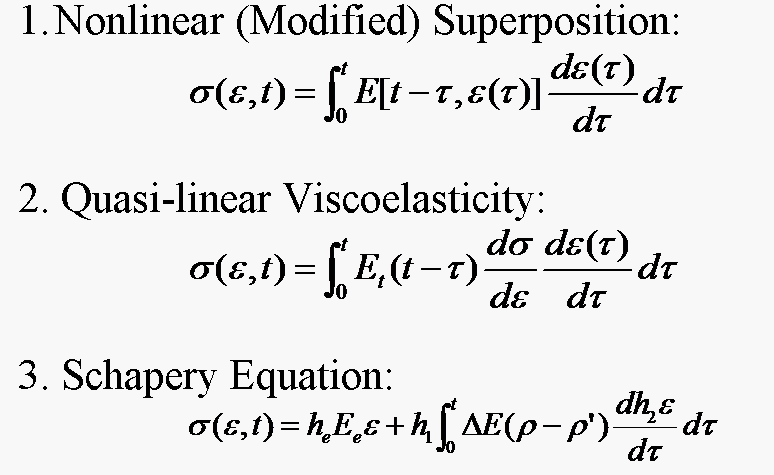
Viscoelasticity class
Viscoelasticity book
Research articles, nonlinear tissue viscoelasticity