Mode Content of Piston-generated Initial Condition

One desirable initial condition for RM experiments is the sine wave since there exist analytical models to calculate the amplitude growth rate in the linear and nonlinear regimes.  Some of these theories may also be used on a multi-mode initial condition by using superposition of modes to calculate growth.  The modal amplitudes will grow at different rates with the higher modes (shorter wavelengths) saturating earliest. Therefore, for comparing experimental growth rates with bubble- or spike-growth models, it is important to have a dominant fundamental mode even if it is not a perfect sine wave.

The He-SF₆ interface generated with the pistons resembles a curtate cycloid, or trochoid.  The parametric equations for a cosine and cycloid are shown below and the condition that a>b means the cycloid is "curtate".

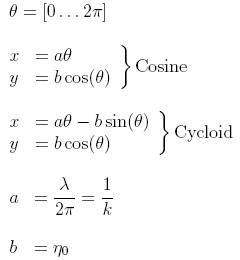
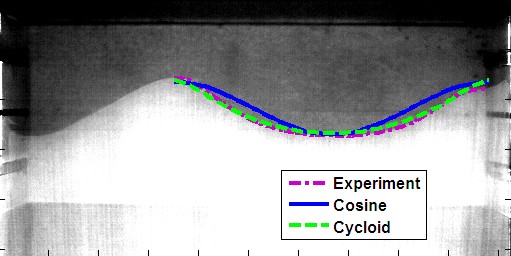
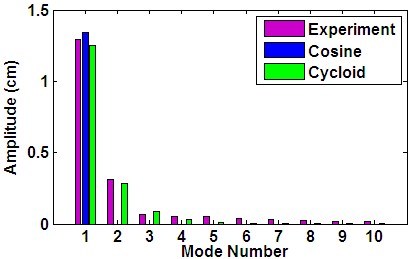
One wavelength of the initial condition is shown below.  The wavelength does not exhibit pure one-fold symmetry.  Also, the starting and ending points are not at the same exact locate, and therefore, the average of these two points and the lowest point on the trough are used to determine a peak-to-peak amplitude of 2&eta₀. An edge detection algorithm is performed on the experimental image to determine the wave and an fft on that wave determines the mode content with only the first 10 being shown in the bar chart. Visually, the cycloid appears to come quite close to the measured interface, and a quantitative comparison may be made by looking at the modal content in the bar chart. Thus, this initial condition is much better described as a cycloid than a cosine as it contains content in modes 2-4 that is close the experimentally measured modes. Also, the fft shows the interface does contain a fundamental dominant mode and is therefore suitable for comparison with many of the analytic theories.