Shocked Bubble Experiments and Computations

Experiments studying the unstable growth of a dense spherical bubble in a gaseous medium, subjected to a strong planar shock wave (2.8 < M < 3.4), are performed in a vertical shock tube. The test gas (argon) is contained in a freely-falling (in N₂) spherical soap-film bubble, and the shocked bubble is imaged using planar laser diagnostics. Concurrently, simulations are carried out using a 3-D compressible hydrodynamics code, Raptor.

Experiments and computations show consistent results, indicating the formation of characteristic vortical structures in the post-shock flow. The results emphasize the significance of 3-D effects, and of small non-uniformities in the initial bubble geometry. Further, the time-behavior of flow features is analyzed, showing that, under some conditions, the development of the unstable interface can be parameterized for variable shock strength.

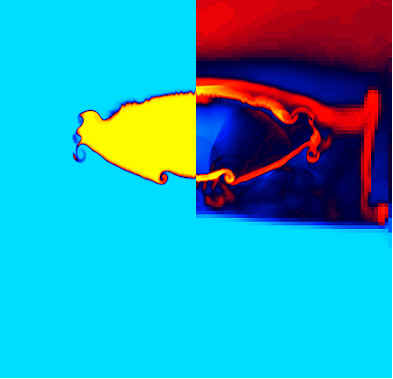
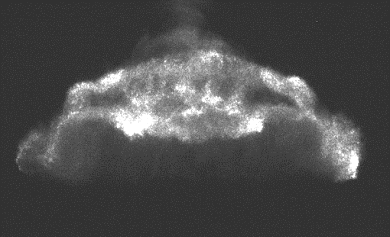
Bubble Development:

Below: Numerical results, Ar volume fraction (left) and total density (right) plots at midplane.

t/t=1.04	t/t=2.42	t/t=3.56	t/t=7.55

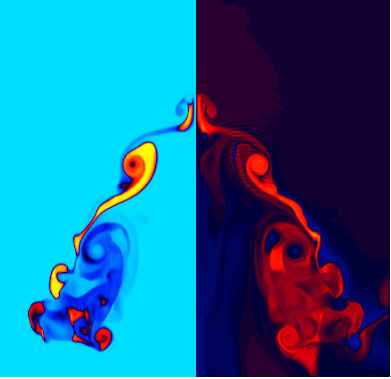
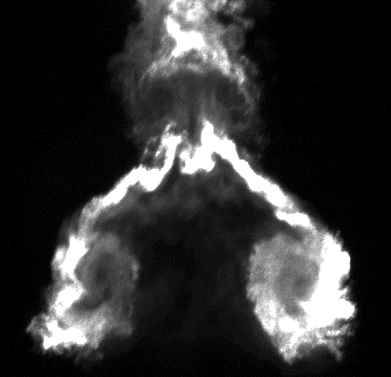
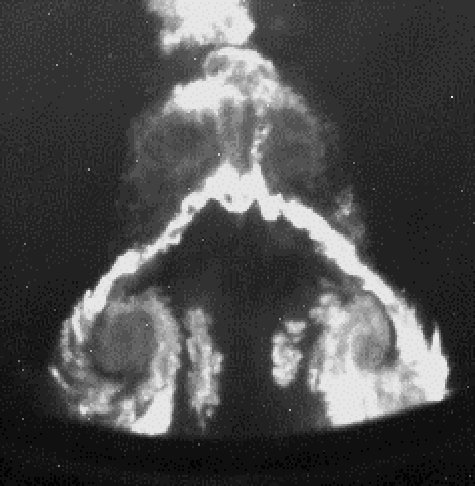
Right: Late-time (t/t=7.91) image and 3-D rendered plot showing multiple vortex rings and complex 3-D structure Blue: Ar vol. fraction=0.1 Red:  vorticity magnitude Green:  film material plotted on cuts

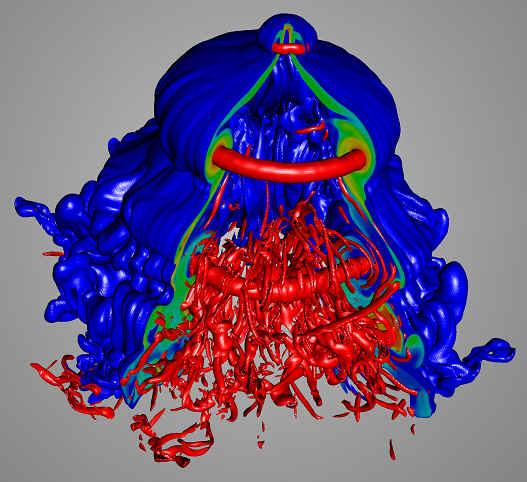3D evolution of the M=2.88 shock accelerating the Ar bubble.  The planar shock wave contacts the top of the bubble and refracts through it.  The bubble is initially compressed into a disk and then the major (and minor) vortex rings are formed as the shock wave moves downstream.  This animation is a reduced version of that which was shown at the 58th annual Division of Fluid Dynamics (DFD) meeting of the American Physical Society (APS), November 20-22, 2005, Chicago, IL during the presentation "Interaction of a planar shock wave with a spherical gas inhomogeneity. Part II: calculations", by John Niederhaus, Devesh Ranjan, Mark Anderson, Jason Oakley, and Riccardo Bonazza. The original high resolution mpeg (1024x1024 pixels, 1356 frames) animation can be downloaded here (huge, 38 MB).  Animation credits from LLNL are:  Jeff Greenough, Hank Childs, Rebecca Springmeyer, and Eugene Cronshagen.

Growth trends:

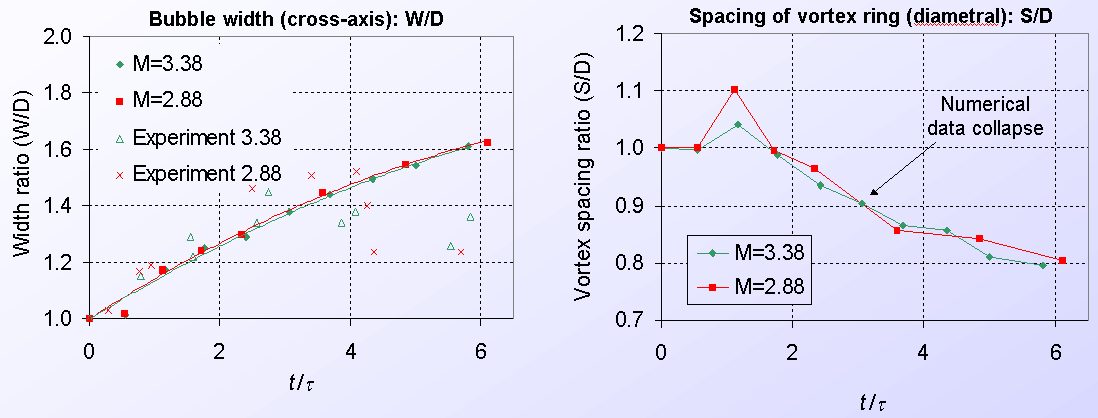
Selected flow features are tracked over time, with parameterization using the shocked particle speed up (t = D/u_p). Flow features shown here are the maximum transverse bubble width (W) and the spacing (S), or primary diameter, of the major vortex ring (numerical only). Reasonable agreement with computations (closed data points) is found for early times (t < 3.5), and both experimental and computational data collapse with this scaling, for these Mach numbers. Further experiments and calculations have shown that such a collapse is not achieved at lower shock strength, where compressibility effects can come into play. 

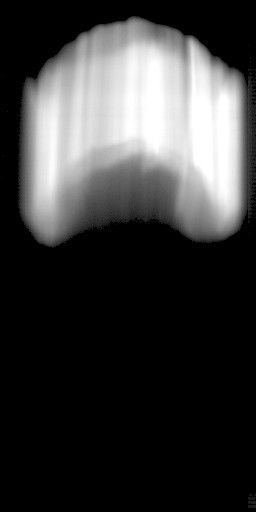
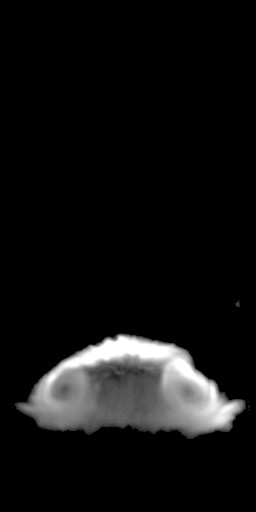
Reshocked Bubble Experiments

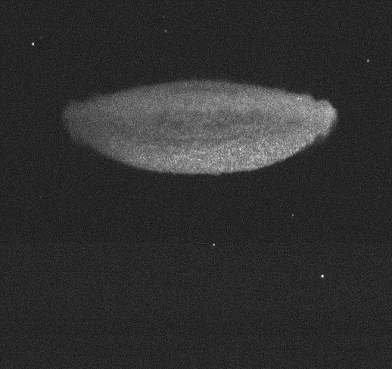
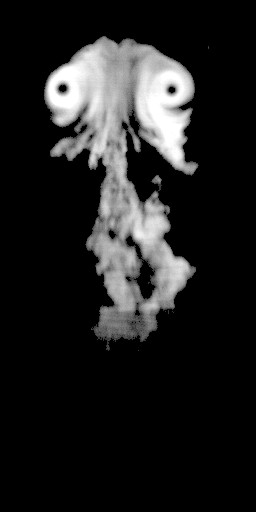
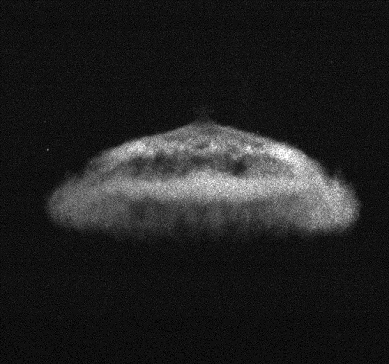
An experiment for a reshocked bubble is shown below. A spherical soap bubble filled with Ar has been accelerated by a M=2 shock wave and is translating downward in a N₂ atmosphere. The bubble appears as a blurred vortex pair in the first image (a) which is a planar cross-section of the vortex ring. The shock wave, which is down-stream of the bubble, is reflected from the end-wall of the shock tube and accelerates the bubble upward. Image (b) is the first image of the reshocked sequence and the blur from this point onward is greatly reduced since the absolute velocity of the bubble is now much smaller. The latest image in the reshock sequence is (c) and a large amount of the bubble mass has been stripped from the vortex ring, however, the ring with its core (which appears black) is still very much intact. An animation (d) of this image sequence at a frame rate of 10 fps (recorded at 10,000 fps) shows the evolution of the reshocked bubble.

(a)	(b)	(c)	(d)

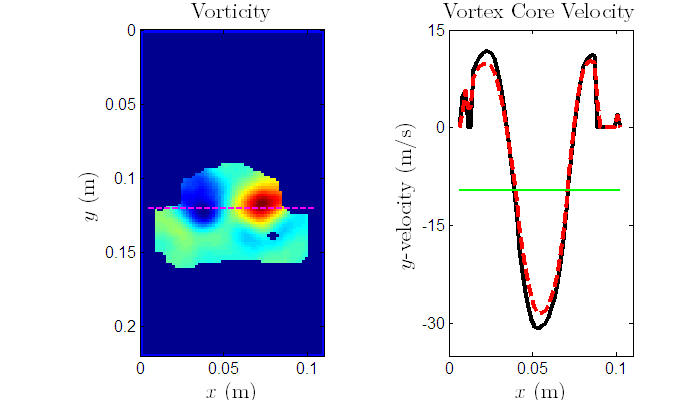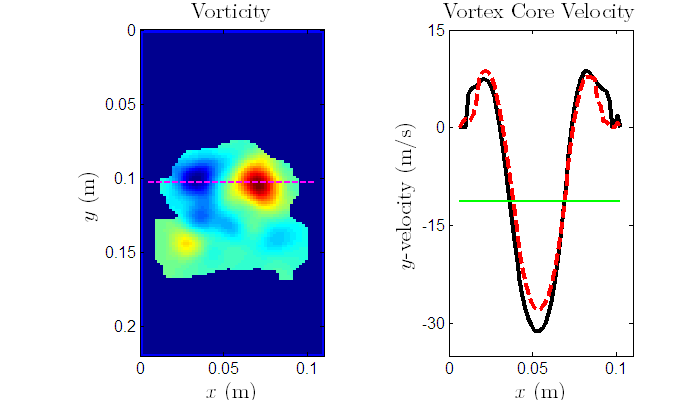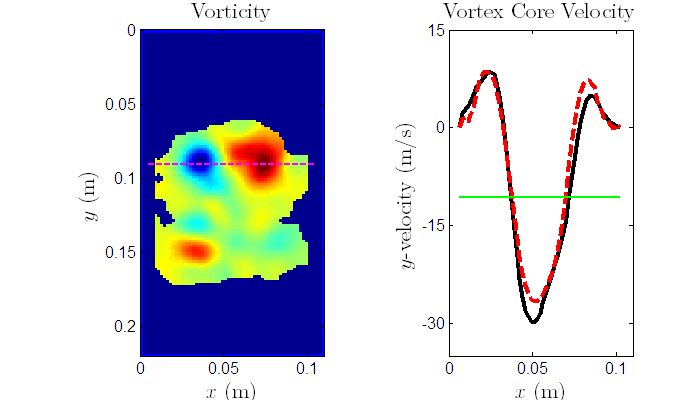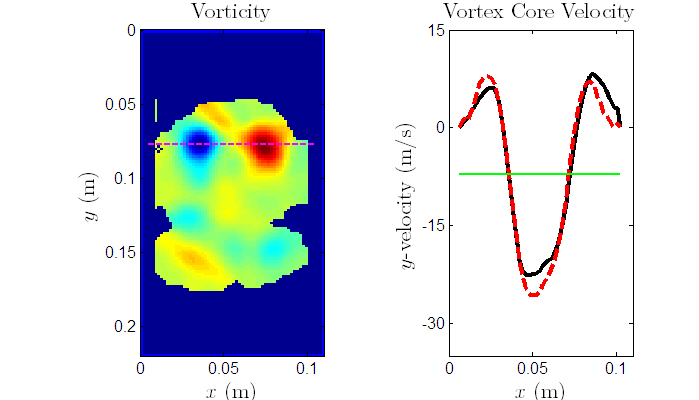
A particle imaging velocimetry (PIV) technique has been performed on a time series of images and is shown below. These data are from an Ar filled soap bubble in a N₂ atmosphere which has been accelerated by a M=1.33 shock wave. The raw data is filtered and smoothed during the PIV operation and from the velocity vector field data the circulation field data is obtained. The horizontal, dashed magenta line in the circulation plot is the average location of the vortex ring's core as determined by averaging the center of the cores on the left and right of the planar image. The y-velocity of the ring cross-section at the core location is plotted to the right of the circulation field. The black line is the velocity at a each time step and the dashed red line is the running average of the velocity at the core location. The cores are moving upward (positive y-velocity) as is apparent in the circulation image movie, but the PIV technique also reveals a stronger velocity field on the ring's axis which is moving in the opposite direction to the core. This is shown as the horizontal green line which is an average of the maximum (typically core location) and minimum (typically axis location) and is negative.