Adapted from the book Viscoelastic Materials and from selected research articles accessible via the main viscoelasticity page above.
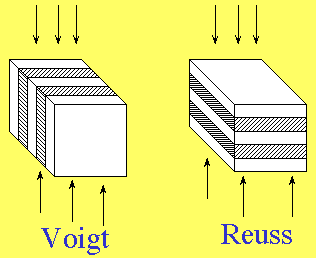
    For an elastic two-phase composite, the stiffness of Voigt and Reuss composites represent rigorous upper and lower bounds on the Young's modulus for a given volume fraction of one phase. There is no restriction on the shape of the two phases. The modulus for the Voigt composite is (neglecting Poisson effects)
E_c = E₁V₁ + E₂V₂,
in which E_c, E₁ and E₂ refer to the Young's modulus of the composite, phase 1 and phase 2, and V₁ and V₂ refer to the volume fraction of phase 1 and phase 2 with V₁+V₂ = 1. This is an exact analytical form for this morphology.
The modulus of the Reuss composite is (neglecting Poisson effects)
1/E_c = V₁/E₁ + V₂/E₂.
    These composite properties are attainable for the structures given. Such laminates are anisotropic since they represent an identical structure subjected to a different orientation of stress. For isotropic composites, the bounds given by Hashin and Shtrikman are applicable; they are tighter than the Voigt-Reuss bounds. Moduli given by the Hashin - Shtrikman formulae are exactly attainable by several hierarchical structures. One is the coated sphere morphology. In this composite the full volume is filled with spheres of different size of one phase; each sphere has a coating of a given fraction of the sphere radius, made of material of the second phase.

    For all the bounds it is tacitly assumed that both phases are in a minimum initial energy state, that is, they have positive stiffness; also that the interface is an ideal attachment with no slip or chemical reactions. Thermoelastic effects are also ignored.
For a viscoelastic composite, use of the dynamic elastic - viscoelastic correspondence principle gives
E*_c = E*₁V₁ + E*₂V₂, in which the * indicates a complex number with magnitude and phase.
Similarly for the Reuss composite, use of the dynamic correspondence principle gives
1/E*_c = V₁/E*₁ + V₂/E*₂.

    To make a map of stiffness vs. mechanical damping (loss tangent), separate the real and imaginary parts and graph the magnitude versus the tangent of the phase. If properties in the time domain (creep or relaxation) are desired, then use the quasi-static elastic - viscoelastic correspondence principle, which gives a convolution form involving the transient properties. For particulate composites including dental composite resins as well as asphalt, stiff mineral inclusions increase the overall stiffness but have little effect on the time-dependent response or on the loss tangent. Particulars are given in the links above.

    Several kinds of composite micro-structure give rise to high stiffness combined with high viscoelastic loss tangent. Two phase composites composed of a stiff, low loss phase and a compliant high loss phase can exhibit high stiffness combined with high loss tangent [1] provided the structure is that of a Reuss laminate, a material containing soft platelets, or a material describable by the Hashin-Shtrikman "lower" formula. The Hashin-Shtrikman formulae for shear modulus G and bulk modulus K provide upper and lower bounds for stiffness vs. volume fraction of elastic isotropic composites. The Hashin-Shtrikman "lower" curve appears in the upper right on a stiffness-loss map, and is close to the Reuss curve, Therefore anisotropy in viscoelastic composites with arbitrary volume fraction differs in its effects from elastic composites with fixed volume fraction. The formulae for the viscoelastic composite are obtained from the elastic formulae by the elastic - viscoelastic correspondence principle. Inclusion of a small amount of damping in the stiff phase has little effect on the composite damping [2]. The bounds [3] for viscoelasticity in the stiffness-loss map either coincide [4,5] with the Hashin-Shtrikman formulae [6,7] or are close to them. If the inclusions have a chemical effect on the matrix, or alter the structure of dislocations or other defects in the matrix, then experiment may not agree with predictions based on the correspondence principle.



Viscoelastic composite plots
  Composite Structure.
  Bounds on composite stiffness.
  Stiffness loss map, theory
  Stiff-loss shape
  Stiff-loss stiff phase
  Experiment, InSn with SiC particles

References
1. Chen, C.P. and Lakes, R.S. (1993). Analysis of high loss viscoelastic composites. J. Materials Science, 28, 4299-4304.
2. Brodt, M. and Lakes, R.S. (1995). Composite materials which exhibit high stiffness and high viscoelastic damping. J. Composite Materials, 29, 1823-1833.
3. Gibiansky, L.V. and Milton, G.W. (1993). On the effective viscoelastic moduli of two phase media: I. Rigorous bounds on the complex bulk modulus. Proc. Royal Soc. London, 440, 163-188.
4. Gibiansky, L.V. and Lakes, R.S. (1993). Bounds on the complex bulk modulus of a two phase viscoelastic composite with arbitrary volume fractions of the components. Mechanics of Materials, 16, 317-331.
5. Gibiansky, L.V. and Lakes, R.S. (1997). Bounds on the complex bulk and shear moduli of a two-dimensional two-phase viscoelastic composite. Mechanics of Materials, 25: 79-95.
6. Schapery, R.A. (1967). Stress analysis of viscoelastic composite materials. J. Composite Materials, 1, 228-267.
7. Hashin, Z. (1965). Viscoelastic behavior of heterogeneous media. J. Appl. Mech., Trans. ASME, 32E, 630-636.