Materials with structural hierarchy

Rod Lakes, University of Wisconsin

Hierarchical structure and its effects
Hierarchical solids contain structural elements which themselves have structure. The hierarchical order of a structure or a material may be defined as the number n of levels of scale with recognized structure. n = 0 corresponds to a material viewed as a continuum for the purpose of analysis of physical properties; n = 1 (first order) could represent a latticework of continuous ribs or the atomic lattice of a crystal. Hierarchical structure can arise in natural and in man made materials. In the latter the structural hierarchy may be intentional or unintentional. The simplest conceptualization of hierarchical structure is descriptive: to recognize that structural features occur on different size scales. At the next level of sophistication, the idea of hierarchical structure can be used in analysis to determine physical properties of the material or the structure. At each level of the structural hierarchy, one may model the material as a continuum for the purpose of analysis. Strictly, such an assumption is warrantable only if the structure size at each level of the hierarchy is very different. Finally, the idea of hierarchical structure can be the basis of the synthesis of new microstructures which give rise to enhanced or useful physical properties. Benefits of hierarchical structure can include improved strength and toughness, or unusual physical properties such as a negative Poisson's ratio.

The idea of macroscopic hierarchical frameworks can be traced back at least to Eiffel's design for his tower [1] (Fig. 1) and of bridges such as the Garabit Viaduct. The Eiffel tower is third order, and has a relative density (density r) as mass per unit volume of the structure divided by density (usually denoted by a Greek rho; if your browser does not handle Symbol font properly, look at the pdf link above) r_o of material of which it is made) r / r_o just 1.2 x 10^-3 times that of of iron [1] which is weaker than structural steel. The rationale for the use of small girders in such a large structure was attributed to ease of construction [2], though it had also been suggested by Mandelbrot [3] that Eiffel perceived a structural advantage. For comparison, we remark that the World Trade Center (New York) and the Pompidou Center (Paris), both first order, n=1, contain a volume fraction of structural steel [4] r / r_o = 5.7 x 10^-3. The World Trade Center contains steel with a yield strain e _y as large as 0.0033, 2 to 3 times as strong as 'mild' structural steel.

A more recent example is a proposal by Dyson [5] to construct hierarchical frameworks in outer space. Dyson presented scaling arguments to the effect that very large structures could be constructed with low mass, however no stress analysis was performed. Stress analysis of elastic buckling in hierarchical truss structures has been performed[6,7]. However, in modern structural engineering the tendency seems to be away from hierarchical structures, since although they contain less material to achieve a desired strength, costs associated with fabrication and maintenance currently exceed any saving in material cost. These structures are considered to be fractal-like, but they are not true fractals since n remains finite and the solid volume fraction does not go to zero even for large n.

Dense hierarchical materials
In this section we discuss hierarchical structure in 'dense' materials with zero or minimal porosity. Both artificial and naturally occurring materials are considered. Hierarchical composite materials are considered.

Composites and polycrystals
Practical fibrous composites commonly have a low order of hierarchical structure in which fibers are embedded in a matrix to form an anisotropic sheet or lamina; such laminae are bonded together to form a laminate (Fig. 2a). In the analysis of fibrous [8,9,10] composites, the fibers and matrix are regarded as continuous media in the analysis of the lamina; the laminae are then regarded as continuous in the analysis of the laminate. The stacking sequence of laminae and the orientation of fibers within them governs the anisotropy of the composite. A similar continuum assumption is used in the analysis of particulate [11] composites and of foams [12]. Inorganic crystalline materials have structural features such as grain boundaries between crystals which are mm to um in size, dislocations, and point defects such as vacancies on the atomic scale; this structure has been studied from a hierarchical perspective [13]. These structural features also give rise to viscoelastic behavior [14,15] manifested as attenuation of stress waves or damping of vibration at different frequencies. Recently polycrystalline materials have been synthesized with a distribution of grain sizes less than 1 micron [16-19] (nanocrystalline materials). The small grain size, hence large interface area, gives rise to desirable properties such as superplasticity (in which large irreversible deformation can occur without fracture), and improved strength and toughness. Small grain size also implies short diffusion distances, so that processes which depend on diffusion, such as sintering, are facilitated and can occur at lower temperatures than would otherwise be possible.

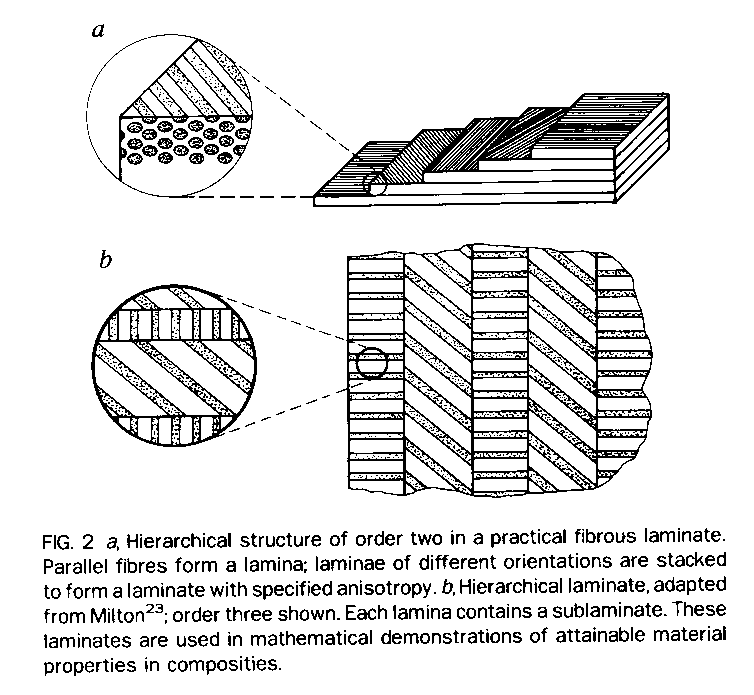
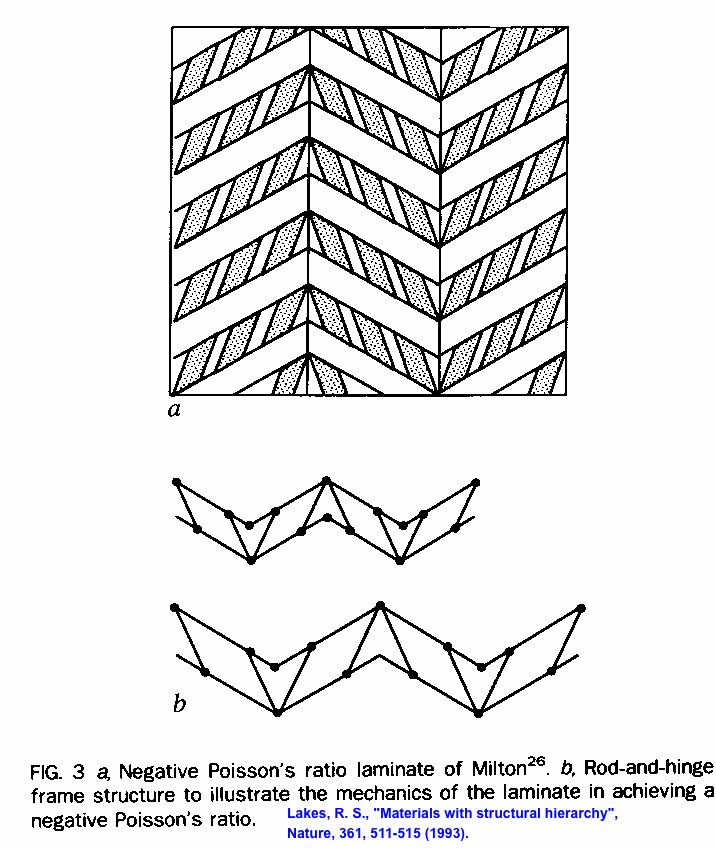
Hierarchical laminate structures have been considered as a vehicle for analytically approximating the stiffness of polycrystalline aggregates [20], for exploring bounds on the electrical conductivity of polycrystals [21-22] and the elastic stiffness of polycrystals [23] and of composites [24]. In these laminates, each lamina is composed of further laminae (Fig. 2b). For elastically isotropic hierarchical laminates, it is possible to attain [24] the theoretical upper or lower bounds [25] on the stiffness. These laminates are considered to be a mathematical tool rather than practical composites since widely differing length scales must be chosen to justify the assumption of each level as a continuum [23]. Negative Poisson's ratios, which imply the material becomes fatter in cross section when stretched, are predicted in hierarchical laminates [26] with a chevron structure (Fig. 3a). The physical mechanism for the unusual Poisson effect is illustrated by the hinged framework which unfolds under tension as shown in Fig. 3b. One can achieve, with these laminates, Poisson's ratio values approaching the lower limit of -1 for mechanically isotropic materials.

Polymers
Polymers can exhibit structural hierarchy on the molecular, ultrastructural, and microstructural levels [27]. In crystalline polymers, there are spherulites on the scale of tens of um; the spherulites themselves contain a lamellar texture and the molecules within the lamellae contain structure. Amorphous polymers have structure on the molecular scale only [27]. However when they are irreversibly deformed, crazes form, and the process can be understood with the aid of a hierarchical approach which can deal with the multiple size scales which appear in the material. Crazes are bridged by microfibrils on the nanoscale, and the microfibril properties are important. At the macroscale the crazed material can be considered as a composite. In covalent amorphous solids, the concept of hierarchical order has been used as an aid in the classification of order at different length scales[28], short range 2-5 Angstroms, medium range 5-20 Angstroms and long range, >=20 Angstroms.

Biological materials
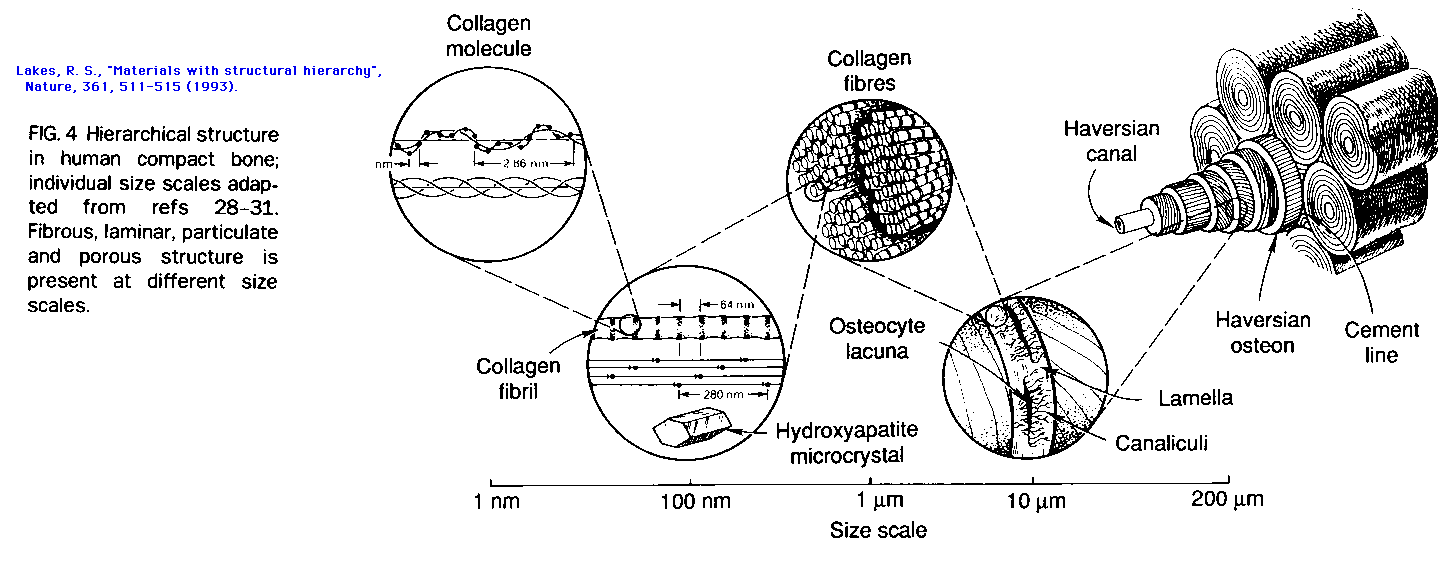
Human compact bone is a natural composite which exhibits a rich hierarchical structure [29-30] (Fig. 4). On the microstructural level are the osteons [31], which are large (200 micron dia.) hollow fibers composed of concentric lamellae and of pores. The lamellae are built of fibers, and the fibers contain fibrils. At the ultrastructural level (nanoscale) the fibers are a composite of the mineral hydroxyapatite and the protein collagen. These specific structural features have been associated with various physical properties. For example, stiffness [32] of bone arises from the composite structure of mineral microcrystals and protein (principally collagen) fibers. Slow creep [33] results from slip at cement lines between osteons. The cement lines as weak interfaces impart a degree of toughness [34] to bone. As for pores, the lacunae are ellipsoidal pores which provide space for the osteocytes, the living cells of bone. The bone cells at this level of scale permit bone tissue to remodel its structure in response to prevailing stresses [35]. Haversian canals are cylindrical pores which contain blood vessels which nourish the tissue. Canaliculi are very fine channels radiating from the lacunae. Mechanical stress in bone due to physical activity is considered to be important in pumping nutrients through these channels [36]. The pore structure of bone is essential in maintaining its viability and consequently its ability to adapt to mechanical stress. A two level hierarchical analytical model [37] has been used to predict anisotropic elasticity of bone; it successfully modeled how bone stiffness depends on the orientation of applied stress with respect to the osteon axis. Other examples of natural hierarchical materials include wood [38-39], tendon [27], trabecular (spongy) bone and bamboo. Of these, only tendon may be regarded as 'dense'; the others are cellular. As for tendon [27], it consists of collagen which on a molecular scale is similar to that of bone. The triple helical collagen macromolecule is formed as a result of the amino acid glycine occupying every third unit. The strongest intermolecular attractions occur when neighboring molecules are shifted by 67 nm, the 'stagger' which is responsible for the banded appearance of collagen observed via electron microscopy. Assembly of subfibrils into fibrils is thought to be controlled at least in part by the primary structure of collagen. In tendon, the collagen forms fibers which are organized into mostly parallel fiber bundles of progressively larger size. The larger scale organization is attributed to interaction with noncollagenous components such as proteoglycan matrix. The fibers are not perfectly aligned; they form a wavy or crimp structure which confers upon the tendon an initial compliance as the fibers straighten under load. Moreover, the damage processes which govern the strength and toughness of tendon involve structural elements over the full hierarchical range of sizes.

Role of the largest structural elements
Structure may be present on many size scales, however the largest structural elements have a unique role in several situations. If the largest structure is not negligible in size compared with the object itself or a crack or hole in the object, the classical continuum view may no longer describe the situation adequately. Objects with large structural elements deformed elastically may exhibit size effects in bending and torsion [40]: slender rods are stiffer than expected classically. The classical prediction is for the rigidity in bending or torsion to be proportional to the fourth power of the diameter. Moreover the magnification of stress (stress concentration) which is predicted in classical elastic solids near holes and notches, is alleviated in some materials with microstructure [40]. Such a phenomenon is beneficial in structural materials. In some foams, incomplete cells near a cut surface contribute to the volume but not to the stiffness or strength [41] so that small objects are less stiff than expected via classical continuum analysis, unlike the slender rod example above. In hierarchical composites the largest size structural elements such as fibers [42-43] or particulate heterogeneities [44] appear to govern the fracture toughness and the localization of microdamage. Classical elasticity theory has no length scale associated with it. More general continuum theories such as Cosserat (micropolar) elasticity allow rotation of points in the continuum as well as translation, and contain characteristic lengths as well as stiffnesses among the material constants. Physically the additional freedom in the continuum corresponds to twisting or bending motions in the fibers or ribs in the material microstructure. Generalized continuum theories offer predictive power in dealing with nonclassical phenomena [40-44]. Such theories may be of use in future analysis of hierarchical materials in which one relaxes the assumption that the structure size at each hierarchical level is very different. Phenomena such as those described above would be expected to occur.

Hierarchical cellular materials
Cellular solids
Cellular solids are composites in which one phase is solid and the other is empty space, or possibly a fluid. Cellular solids occur in nature in rocks, wood, and bone. Porous rocks can exhibit a wide range of pore sizes [45], but the structure is not as highly organized as that of wood and bone. Wood contains elongated pores (called tracheids or fibres) oriented along the tree or limb axis; radial channels called rays, and larger sap channels [12,46]. The cell walls are themselves fibrous and consist of oriented cellulose in a hemicellulose and lignin matrix. The alignment of the tracheids is favorable for resisting the prevailing forces in the tree [12]. Trabecular bone has a spongy structure. The struts or ribs in trabecular bone have a complex internal structure similar to that of the osteon in compact bone referred to above; see also Fig. 4.

Cellular solids are made as synthetic materials used for applications such as cushioning, filtration, insulation and lightweight sandwich cores. Cellular solids may have a two dimensional structure, as in honeycombs, or a three dimensional structure as in foams. In most synthetic cellular solids, there is only one size scale aside from the atomic: that of the cells. Examples of cellular solids which have hierarchical structure are as follows. Some synthetic open cell polymer foams can have an unintentional hierarchical structure in that the ribs may contain 'microcells'[47]. Aerogels are gels with the fluid phase as air rather than water; they have submicroscopic pores with a wide range of sizes organized in a hierarchical structure [48,49]. The microstructure depends upon density so that Young's modulus varies as the 3.8 power of density. Negative Poisson's ratio foams [50], which become fatter in cross section when stretched, have an inverted (re-entrant) cell shape in which the cell ribs bulge inward rather than outward. They are not hierarchical, however they may be used to make hierarchical composites in which the open space in the cells is filled with a compliant solid or with a foam of smaller cell size. If the filler is viscoelastic, the composite's viscoelastic response can be made large if the filler experience a larger local strain than does the composite. It is possible to design materials in which Poisson's ratio increases or decreases [51] with time by choice of the relaxation rates of the large cell foam and the filler foam. Intentional hierarchical structure appears in the designs of Eiffel [1] and in a proposal by Dyson [5]. The first quantitative analysis of open hierarchical structures known to the writer is that of Parkhouse [6], and the subject was treated in a design competition [7]. Lattice, truss, honeycomb and tubular geometries were considered, and it was shown that hierarchical structure can be used in the design of structural elements which, for a given compressive strength, are much lighter than elements with simple structure. The effect of damage on reliability in homogeneous solids and in structures with one scale size and those with hierarchical structure were described [52] in connection with continuum models of structures. This work was adduced in a review [53] which elucidated the freedom which a designer of load bearing components has in choosing material properties, section shape, and with cellular and composite materials, microstructural degrees of freedom.

Prediction of strength and stiffness of hierarchical cellular solids
In cellular materials, the stiffness depends on density and upon the structure. In many such materials, which ordinarily exhibit structure on only one level of scale, the scale of the cells, the relationships are simple. The Young's modulus (stiffness) E of a cellular material such as a foam or honeycomb (considered as a continuum) is given in terms of the Young's modulus Eo of the solid from which the material is made, the density r₀ of the solid phase, and the density r of the foam [12]. The atomic structure is ignored here since it is absorbed in the continuum description of the cell ribs.

E/E_o = k[r /r₀] ^r       (Equation 1)

The values of k and r depend on the type of structure (Table 1). In this section, stiffness and strength in hierarchical cellular solids is predicted for 'conventional' (not re-entrant) materials: honeycombs with hexagonal cells and for open cell foams with convex (usually tetrakaidecahedral) cells. Analysis is facilitated by the recent availability of simple continuum models of cellular solids[12]. Hierarchical cellular solids are considered in which the material making up the cell ribs is also cellular and has a smaller cell size. The hierarchical order n of a material may be defined as the number of levels of scale in the hierarchy. For a solid material viewed as a continuum, n=0, for a conventional foam or honeycomb, n=1, and for a sponge with porous ribs, n=2. Hierarchical solids may be envisaged with any hierarchical order, with an upper bound on n determined by the fact that the smallest cells must be of larger size than atomic dimensions.

To predict the properties of hierarchical cellular solids, we cascade the stiffness equation (1), considering the solid density to be r₀ at zeroth order. Strictly, the classical continuum view used here is warrantable only if the size of the structure making up each cell wall or rib is much smaller than the rib itself.

E_n/E_o = kⁿ [r /r₀] ^r       (Equation 2)

Based on Eq. 2, for honeycombs deformed out of plane and for foams (k=1), the hierarchical order n does not influence the stiffness, while for framework type structures for which k<1 the stiffness decreases with n. The relationships for compressive strength [12] s, or maximum stress prior to collapse, of conventional first order materials (n=1 for cellular material, n=0 for the solid phase) are rewritten here in a general form for several failure mechanisms and for two arbitrary hierarchical orders differing by one, with n>=1. Here 'a' and 'q' are parameters which depend on the rib failure mode and material structure, see Table 1 (Not in the html version).

s_n = a k E_n-1 [r_n / r _n-1]^q       (Equation 3)

Possible failure mechanisms are elastic buckling of cell ribs in which the ribs reversibly collapse, plastic buckling in which the ribs irreversibly collapse, or crushing in which the ribs fracture. As shown in Table 1, the strength parameter 'a' for plastic buckling in Eq. 3 depends on e_y,solid, the strain at yield for the solid from which the material is made; for crushing, it depends on e_ult,solid, the fracture strain of the solid. After some manipulations, and assuming the density ratio is the same for each level, the strength to density ratio of the hierarchical material is, for n>=1:

The strength to density ratio is bounded from above by that of the solid at the zeroth level of the hierarchy. In Eq. 4 the crush limit for honeycomb is seen to be independent of hierarchical order, since k = 1 and q = r = 1, n has no effect.

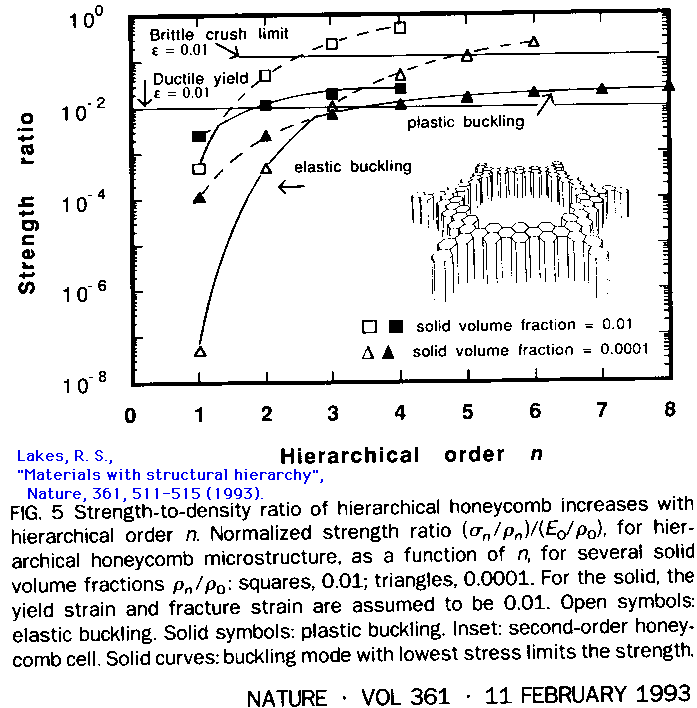
Predicted strength to density ratio of honeycombs is shown in Fig. 5. The physical mechanism for the improved strength is the suppression of buckling in the hierarchical structure. Since failure can occur by elastic buckling, plastic buckling or crushing, the actual strength corresponds to the lowest stress of the possible failure modes. Observe that for low density honeycombs, a very dramatic improvement in compressive strength can be realized in hierarchical structures. Most of the gain in strength occurs in the first few orders; the situation for large hierarchical order n is one of diminishing returns. Moreover, the relative thickness of the cell walls increases with n, so for a relative density of 0.01, values of n above 4 are unrealistic. In Fig. 5, yield or brittle fracture of the solid phase is assumed at a strain [[epsilon]] of 0.01, a value representative of a high strength steel or of a high performance fibrous composite. If the solid phase had a higher ultimate strain, (e.g. e_ult = 0.054 for glass fibers; 0.08 for silica) the transition from elastic buckling to plastic buckling in Fig. 5 would occur at higher stress. Consequently, there is a significant advantage to using high strength materials in making a hierarchical honeycomb, in contrast to conventional honeycomb in which only the stiffness of the solid phase is important.

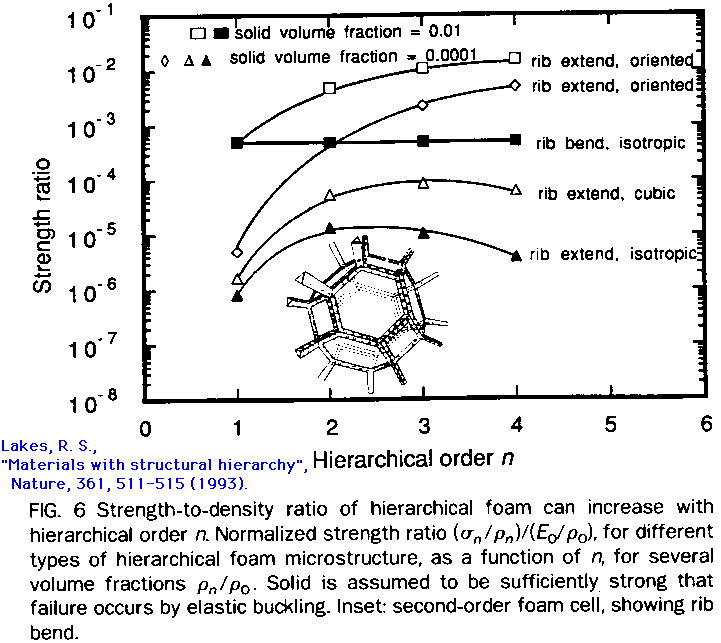
As for foams, conventional open cell foams deform via rib bending [12] for which r=2 and k=1 in Eq. 1. For such foams, there is no strength advantage associated with the hierarchical structure, as shown in Fig. 6. The situation is different for an oriented foam [12,54] such as trabecular (spongy) bone of a particular structure (modeled as first order) in which deformation proceeds by axial rib extension with r=1 and k=1 in Eq. 1. A cubic lattice of beams (k = 1/3), more representative of building construction than of foams, deforms axially in this way. Such materials and structures are predicted to exhibit a significant strength advantage associated with the hierarchical structure, as shown in Fig. 6. For large n, the cubic and isotropic microstructures do not perform as well since at each level, some ribs are oriented so that they do not support load. Hierarchical cellular solids represent a form of hierarchical composite in which one phase is empty space.

As for macroscopic hierarchical structures, predictions of stiffness and strength are independent of scale and are relevant to large structures as well. Large structures can be made using less weight of metal if made in hierarchical form. If only the possibility of elastic buckling were considered as in Ref. 6, the saving in strength or weight of these structures would be overestimated.

A different type of analysis which gives rise to hierarchical structure is finite element analysis in which the topology of a structural element is allowed to vary [55]. In finite element analysis a computer is used to analyze stress and deformation fields in an object by subdividing a model of the object into many small segments for which it is simple to compute stress. In most applications of the method, boundaries of the model are not changed. In the work cited, holes were deliberately introduced in the model, and the holes' boundaries progressively modified depending on the calculated stress at each iteration. Optimization of the structural element to maximize stiffness for given weight leads to a cellular microstructure which becomes truss-like if the solid volume fraction is small. The optimal microstructure under some conditions is hierarchical.

In this segment, some new experimental results on hierarchical honeycomb are presented. Hierarchical honeycombs of second order can easily be made by the same techniques currently used to make practical expanded honeycomb. In the hobe (honeycomb before expanding) block method, strips of material are bonded together via bands of adhesive so that the bonded regions of one strip lay above the unbonded regions of adjacent strips. The width of glued and unglued sections is made equal if regular hexagons are desired in the final honeycomb. The stack of strips is pulled apart so that the web between the bonded strips forms the cell walls. In the present study, a modified hobe block approach was used to make hierarchical honeycomb by stacking unexpanded small cell layers and using wide glue strips between them to make large cells with small cells in the walls. Hierarchical honeycomb was also made by cementing segments of first order honeycomb to form a larger honeycomb. Experiments using a servohydraulic test machine to crush the specimens disclosed second order paper honeycomb to be a factor 3.2 to 3.8 stronger in compression than first order honeycomb of the same density 0.01 g/cm^3. The simple theory developed above, assuming plastic buckling, predicts a strength enhancement of a factor of 4.6. Given the idealizations involved, including identical density ratio at each order, the correspondence is considered adequate. Honeycomb made of a stronger material would be enhanced even more in strength by hierarchical structure, since the transition between the governing failure modes depends on the strength of the material used.

Conclusions and prospects
Many materials exhibit hierarchical structure; the hierarchical aspects of structure can be considered for descriptive purposes, for analysis and for synthesis. Hierarchical cellular material microstructures can exhibit dramatic increases in compressive strength compared with that of cellular solids of similar density with conventional structure. Two-dimensional hierarchical cellular solids (honeycombs) are straightforward to make. Manufacture of other hierarchical cellular solids could be accomplished via rapid prototyping systems [56] in which a computer generated design may be converted into complex shapes by photochemical, sintering, deposition, layering, or sculpting techniques. We envisage applications of hierarchical honeycomb in lightweight sandwich panels. The concept of hierarchical structure is likely to be useful as a guide for the synthesis of other new material microstructures giving rise to significant improvement in useful material properties. An intriguing possibility is that of simultaneously achieving high values of strength and toughness, for which ordinarily there is a trade-off. Hierarchical structure can also permit one to achieve extremal values of unusual properties such as negative Poisson's ratios. There is the further possibility of designing new materials with extreme values of other physical properties such as thermal expansion or piezoelectricity.

I thank the University of Iowa for a University Faculty Scholar award; and the Department of Engineering Mechanics at the University of Wisconsin and the Department of Theoretical and Applied Mechanics at Cornell University where part of this work was conducted. I thank Professors D. Branson and A. Bhatti for discussions on structural engineering; D. Lakes and A. Suliman for aid in preparing specimens; and J. B. Choi for materials testing. Partial support by the NASA/ Boeing ATCAS program under contract #NAS1-18889, and by ONR, is gratefully acknowledged.

FIGURES

1 Hierarchical structure in the Eiffel tower, after Loyrette [1].

2 (a) Hierarchical structure of order two in a practical fibrous laminate. Parallel fibers form a lamina; laminae of different orientations are stacked to form a laminate with specified anisotropy.

(b) Hierarchical laminate, adapted from Milton [23]; order three shown. Each lamina contains a sub-laminate. These laminates are used in mathematical demonstrations of attainable material properties in composites.

3. (a) Negative Poisson's ratio laminate of Milton [26].

(b) Rod and hinge frame structure to illustrate the mechanics of the laminate in achieving a negative Poisson's ratio.

4 Hierarchical structure in human compact bone; individual size scales adapted from Refs 28-31. Fibrous, laminar, particulate, and porous structure is present at different size scales.

5 Strength to density ratio of hierarchical honeycomb increases with hierarchical order n. Normalized strength ratio, for hierarchical honeycomb microstructure, as a function of hierarchical order n, for several solid volume fractions: squares, 0.01; triangles 0.0001. For the solid the yield strain and fracture strain are assumed to be 0.01. Open symbols: elastic buckling. Solid symbols: plastic buckling. Inset: second order honeycomb cell. Solid curves: buckling mode with lowest stress limits the strength.

6 Strength to density ratio of hierarchical foam increases with hierarchical order n. Normalized strength ratio, for different types of hierarchical foam microstructure, as a function of hierarchical order n, for several solid volume fractions. Solid is assumed to be sufficiently strong that failure occurs by elastic buckling. Inset: second order foam cell exhibiting rib bend.

Rod Lakes