Foam structures with a negative Poisson's ratio
adapted from
Science,
235 1038-1040 (1987).
Download
pdf.
A novel foam structure is presented, which exhibits a negative Poisson's ratio. Such a material expands laterally when stretched, in contrast to ordinary materials. In later years, various terminology has become popular. For example, a metamaterial is a solid made by humans in which anomalous or high values of material properties arise from structure rather than chemical composition. Metamaterial is a word that has recently become popular. We did not call it a metamaterial. The term auxetic was introduced in the U. K. in a later proposal for negative Poisson's ratio polymers. We did not use the phrase material by design.
Virtually all common materials undergo a transverse contraction when stretched in one direction and a transverse expansion when compressed. The magnitude of this transverse deformation is governed by a material property known as Poisson's ratio. Poisson's ratio is defined as minus the transverse strain divided by the axial strain in the direction of stretching force. Since ordinary materials contract laterally when stretched and expand laterally when compressed, Poisson's ratio for such materials is positive. Poisson's ratios, denoted by a Greek nu, n, for various materials are approximately 0.5 for rubbers and for soft biological tissues, 0.45 for lead, 0.33 for aluminum, 0.27 for common steels, 0.1 to 0.4 for cellular solids such as typical polymer foams, and nearly zero for cork.
Negative Poisson's ratios are theoretically permissible but have not, with few exceptions, been observed in real materials. Specifically, in an isotropic material (a material which does not have a preferred orientation) the allowable range of Poisson's ratio is from -1.0 to +0.5, based on thermodynamic considerations of strain energy in the theory of elasticity(1). It is believed by many that materials with negative values of Poisson's ratio are unknown (1); however Love (2) presents a single example of cubic 'single crystal' pyrite as having a Poisson's ratio of -0.14; he suggests the effect may result from a twinned crystal. Analysis of the tensorial elastic constants of anisotropic single crystal cadmium suggests Poisson's ratio may attain negative values in some directions(3). Anisotropic, macroscopic two-dimensional flexible models of certain honeycomb structures (not materials) have exhibited negative Poisson's ratios in some directions(4) . These known examples of negative Poisson's ratios all depend on the presence of a high degree of anisotropy; the effect only occurs in some directions and may be dominated by coupling between stretching force and shear deformation. The materials described in the following, by contrast, need not be anisotropic.

Fig. 1. Conventional open cell polymer foam. Scale mark: 2 mm. The original shows a stereo pair.
Foams with negative Poisson's ratios were produced from conventional low density open-cell polymer foams (Fig. 1) by causing the ribs of each cell to permanently protrude inward, resulting in a re-entrant structure such as that shown in Fig. 2.

Fig. 2 Re-entrant foam. Permanent volumetric compression is a factor of 2.7.
Poisson's ratio is -0.6. Scale mark: 2 mm. The original shows a stereo pair.
An idealized re-entrant unit cell is shown in Fig. 3.
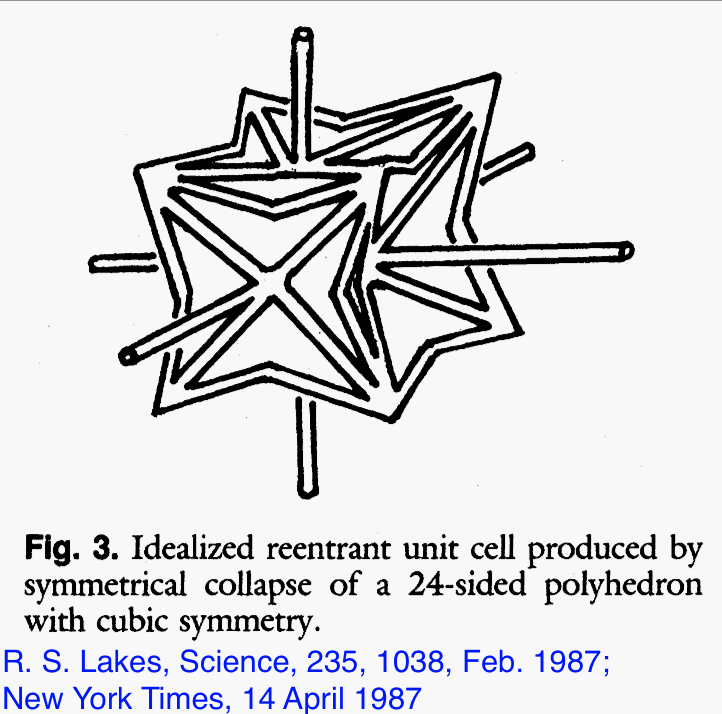
Fig. 3. Idealized re-entrant unit cell produced by symmetrical collapse of a 24-sided polyhedron with cubic symmetry.
A polyester foam (5) was used as a starting material and was found to have a density of 0.03 gm/cubic cm, a Young's modulus of 71 kPa (10 psi), a cell size of 1.2 mm, and a Poisson's ratio of 0.4. The method used to create the re-entrant structure is as follows. Specimens of conventional foam were compressed triaxially, i.e. in three orthogonal directions, and were placed in a mold. The mold was heated to a temperature slightly above the softening temperature of the foam material, 163 deg. C to 171 deg. C in this case. The mold was then
cooled to room temperature and the foam was extracted. Specimens which were given a permanent volumetric compression of a factor of 1.4 to a factor of 4 during this transformation process were found to exhibit negative Poisson's ratios. For example, a foam subjected to a permanent volumetric compression of a factor of two had a Young's modulus of 72 kPa, and a Poisson's ratio of -0.7. Polyester foams of similar structure and properties but different cell sizes (0.3 mm, 0.4 mm, 2.5 mm) transformed by the above procedure were also found to exhibit negative Poisson's ratios. Reticulated metal foams were transformed by the alternate procedure of plastically deforming the material at room temperature. Permanent compressions were performed sequentially in each of three orthogonal directions. Foams transformed in this way were also found to exhibit re-entrant structures.
The casual observer may comment that materials with negative Poisson's ratios are counterintuitive in that they do not conserve volume. This is not objectionable since there is no law of conservation of volume. Various observers develop physical insight from rubbery materials which are indeed nearly incompressible. Nevertheless, such common materials such as steel, aluminum, conventional foams, and hard plastics have Poisson's ratios which differ from 0.5, hence these materials do not 'conserve volume'. All known materials, including the ones described here, obey conservation of energy, which restricts Poisson's ratio to be between -1 and 0.5 for isotropic materials. The physical origin of the negative Poisson's ratio can be appreciated in view of the idealized unit cell shown in Fig. 3. Tension applied to the vertical links will cause the cell to unfold and expand laterally. The actual cell structure (Fig. 2) also contains ribs which are bent and protrude into the cells.
Foams with negative Poisson's ratios were found to be more resilient than conventional foams. Foams with a typical structure of tetrakaidecahedral (14-sided) cells (6) exhibit a reasonably linear compressive stress-strain curve up to about 5% strain (7). At higher strains, the cell ribs buckle and the foam collapses at constant stress. Re-entrant foams exhibited a reasonably linear relationship between stress and strain up to more than 40% strain, with no abrupt collapse. Resilience was enhanced for deformation in each of three orthogonal directions. Improved resilience (in one direction) has also been reported in foams compressed permanently in one direction (uniaxially) (8). I prepared such foams and found them to exhibit Poisson's ratios of near zero. They did not exhibit negative values.
It is notable that the theory of elasticity contains no characteristic length scale. The phenomenon of a negative Poisson's ratio consequently does not require a coarse cellular structure or depend on the structure size. In principle, materials with microstructure on a scale smaller than 1 μ m could exhibit a negative Poisson's ratio. The theory of elasticity also predicts a variety of unusual phenomena to occur in solids with a negative Poisson's ratio. For example, the top and bottom lateral surfaces of a bent prismatic beam of a conventional material with a positive Poisson's ratio assume a saddle shape: the 'anticlastic curvature' of bending, in which the transverse curvature is opposite the principal curvature of bending (9). In the case of a negative Poisson's ratio, the theory of elasticity predicts that these surfaces will assume an ellipsoidal shape, or a synclastic curvature. I have observed such synclastic curvature in bent bars of transformed foam. Furthermore, in the indentation of a block of material by a localized pressure distribution, the indentation for a given pressure is proportional to (1 - n 2)/E in which E is Young's modulus and n is Poisson's ratio. Consequently, a material with a negative Poisson's ratio approaching the thermodynamic limit -1 will be difficult to indent even if the material
is compliant. The origin of this predicted phenomenon may be traced to the relation between the shear modulus G, the bulk modulus B (the inverse of the compressibility) and Poisson's ratio n: B = 2G(1 + n)/(1 - 2n). When the Poisson's ratio approaches 1/2, as in rubbery solids, the bulk modulus greatly exceeds the shear modulus and the material is referred to as incompressible. When the Poisson's ratio approaches -1, the material becomes highly compressible; its bulk modulus is much less than its shear modulus. The toughness of a material can also depend on its Poisson's ratio. Specifically, the critical tensile stress (10) for fracture of a solid of surface tension T, Young's modulus E, with a plane circular crack of radius r goes as the square root of pET / 2r(1 - n 2) , with p = 3.15159.... When the Poisson's ratio approaches -1, the material is predicted to become very tough.
Applications of novel, re-entrant foams with negative Poisson's ratios may be envisaged in view of the above. An example of the practical application of a particular value of Poisson's ratio is the cork of a wine bottle. The cork must be easily inserted and removed, yet it also must withstand the pressure from within the bottle. Rubber, with a Poisson's ratio of 0.5, could not be used for this purpose because it would expand when compressed into the neck of the bottle and would jam. Cork, by contrast, with a Poisson's ratio of nearly zero, is ideal in this application. It is anticipated that re-entrant foams may be used in such applications as sponges, robust shock absorbing material, air filters, and fasteners.
Top
References and notes
1. Y.C. Fung, Foundations of solid mechanics, (Prentice Hall, 1968), p.353.
2. A.E.H. Love, A treatise on the mathematical theory of elasticity, (Dover,1944) 4th ed.
3. Y. Li, Phys. Status Solidi 38, 171 (1976).
4 L. J. Gibson, M. F. Ashby, G. S. Schajer, and C. I. Robertson, Proc. Royal Society London, A382, 25 (1982)
5. Scott Industrial Foam, Scott Paper Co. Specimens kindly supplied by Foamade Industries,
Auburn Hills, MI.
6. L. Holliday, ed., Composite Materials, Elsevier, 1966. Ch. 6, "Thermoplastic systems", by H. A. Lanceley, J. Mann, and G. Pogany.
7. Ashby, M.F., Metallurgical Transactions, 14A,1755 (1983).
8. W. R. Powers, U.S. Patent #3,025,200, 1962.
9. S. P. Timoshenko and J. N. Goodier, Theory of Elasticity, (McGraw Hill, 1982) 3rd Ed.
10 I. N. Sneddon, Fourier Transforms, (McGraw Hill, 1951).
Top


