Cosserat Elasticity; micropolar elasticity
more freedom than classical elasticity
The Cosserat theory of elasticity, also known as micropolar elasticity, the micropolar theory of elasticity, or micropolar continuum mechanics, incorporates a local rotation of points as well as the translation assumed in classical elasticity; and a couple stress (a torque per unit area) as well as the force stress (force per unit area). The force stress is referred to simply as 'stress' in classical elasticity in which there is no other kind of stress. The idea of a couple stress can be traced to Voigt during the early development of the theory of elasticity. More recently, theories incorporating couple stresses were developed using the full capabilities of modern continuum mechanics. Early theoretical work was done by the Cosserat brothers, by Mindlin, and by Nowacki. Eringen incorporated micro-inertia (which allows incorporation of dynamic effects) and renamed Cosserat elasticity micropolar elasticity.
Generalized continuum theories such as Cosserat elasticity are pertinent to the performance of materials because a reduction in stress concentration factor around holes and cracks is predicted. This can give rise to improved toughness. In the following, we present experimental results for materials with microstructure.
In the isotropic Cosserat solid or micropolar continuum, there are six elastic constants, in contrast to the classical elastic solid in which there are two, and the uniconstant material in which there is one. Cosserat elasticity may be viewed as a particular manifestation of nonlocality, but is not equivalent to the general nonlocal elasticity. Strain gradient effects occur. Cosserat elasticity accommodates size effects in elastic behavior; it is more general than the gradient plasticity theory paradigm used to model size effects in plasticity. In multiscale modeling, Cosserat effects are expected to appear as the consequence of the largest structural elements in the material. Multiscale modeling does not, however, allow prediction of Cosserat effects in complex composites such as those of biological origin because the properties of all constituents are not well characterized. Cosserat elasticity entails sensitivity to strain gradient. New phenomena are predicted that are not anticipated in strain gradient models. Experiment is especially called for in such cases. In Cosserat elasticity, elastic constants obtained in different experimental modalities have been compared successfully for internal consistency.
Bottom: recent articles
Research, mostly experimental, is presented below in aspects of composite materials, micromechanics, cellular solids, and biological materials which can be understood via Cosserat (or micropolar) elasticity. We experimentally determine the Cosserat elastic constants, and demonstrate the predictive power of Cosserat elasticity in correctly predicting strain distribution using elastic constants determined by the method of size effects as shown in the diagram below. Selected materials with microstructure are shown experimentally to obey micropolar theory rather than classical elasticity. Micropolar elastic constants are determined via experiments. If desired these may be converted into bending and curvature moduli associated with the Mindlin couple stress theory which is a special case of Cosserat elasticity.
Get pdf of a review article. Lakes, R. S., "Experimental methods for study of Cosserat elastic solids and other generalized continua", in Continuum models for materials with micro-structure, ed. H. Muhlhaus, J. Wiley, N. Y. Ch. 1, p. 1-22, (1995). Material constants of micropolar materials or Cosserat elastic solids are determined via experiment.
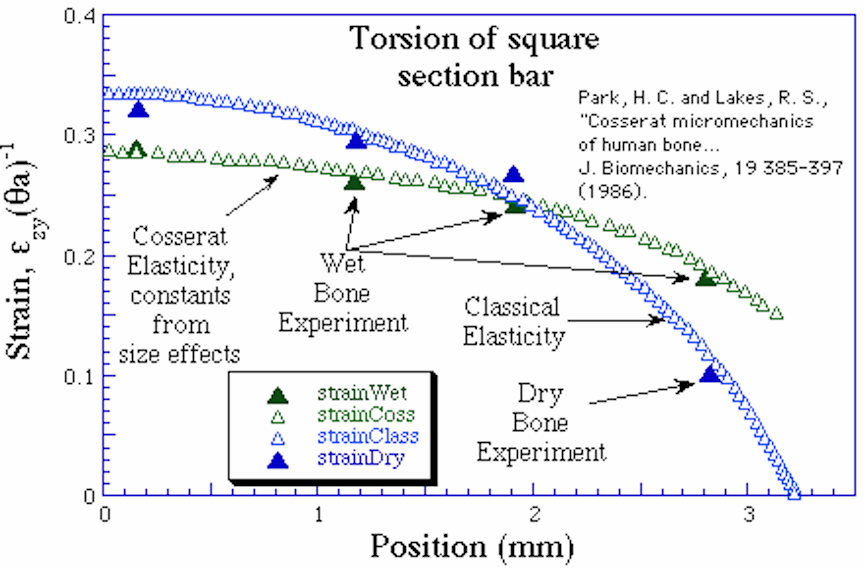
This diagram shows the distribution of strain measured in the torsion of a prismatic specimen of bone, of square cross section. Shown for comparison is the theoretical strain distribution according to classical elasticity. That strain vanishes at the corner of the cross section. Also shown is the theoretical strain distribution according to Cosserat elasticity. The elastic constants used for the calculation were determined in independent measurements of size effects on wet bone. The predictive power of Cosserat elasticity is illustrated. Wet bone follows the Cosserat curve. Strain is redistributed from peak regions to regions which are classically forbidden so that stress concentration is ameliorated for bone.

Cosserat equations using symbols after Eringen. Click on image for larger image. Here is a table of symbols used by different authors.
Couple stress theory is a special case for κ tending to infinity, much larger than the shear modulus.
Classical elasticity is, according to its name, the currently accepted theory of elasticity.
The following behavior is predicted.
(i) The rigidity of circular cylindrical bars of diameter d in tension is proportional to the square of the diameter; in bending and torsion, the rigidity is proportional to the fourth power of the diameter.
(ii) The wave speed of plane shear waves and dilatational waves in an unbounded medium is independent of frequency.
(iii) There is no length scale in classical elasticity, hence stress concentration factors for holes or inclusions in an infinite domain under a uniform stress field depend only on the shape of the inhomogeneity, not on its size.
Cosserat or micropolar elasticity has the following consequences in isotropic materials.
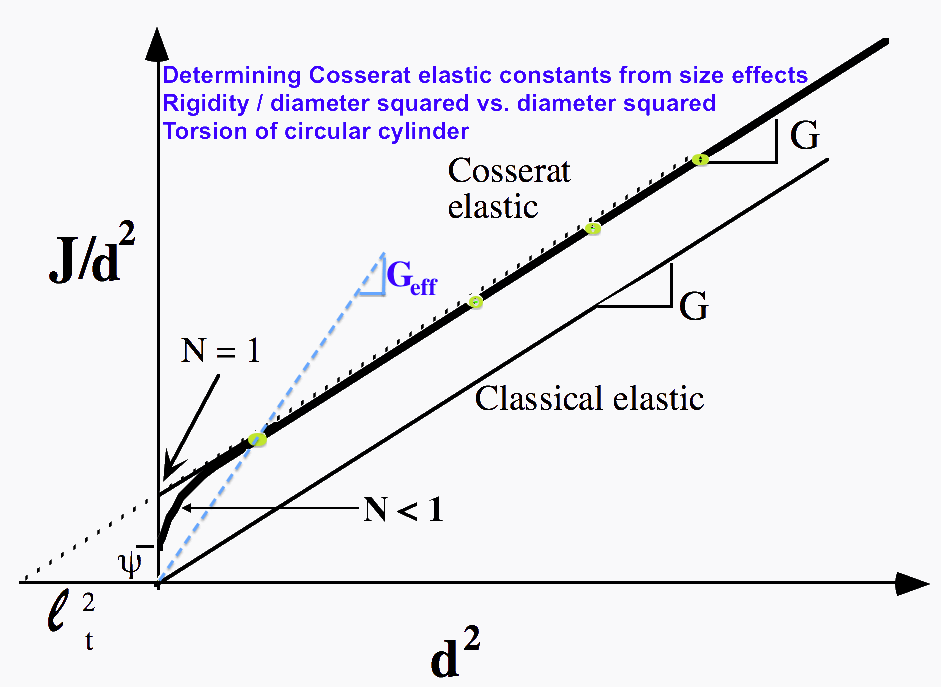
(i) A size-effect [see experimental Cosserat figure] is predicted in the torsion of circular cylinders and of square section bars of Cosserat elastic materials. Slender cylinders appear more stiff then expected classically. There is a sensitivity to strain gradient. A similar size effect is also predicted in the bending of plates and of beams. In experimental Cosserat elasticity, one uses these size effects to determine the characteristic lengths. No elastic size effect is predicted in tension.
(ii) The stress concentration factor for a circular hole, is smaller than the classical value. Small holes exhibit less stress concentration than larger ones. This gives rise to enhanced toughness.
(iii) The wave speed of plane dilatational waves in an unbounded Cosserat elastic medium is independent of frequency as in the classical case. The speed of shear waves depends on frequency in a Cosserat solid. A new kind of wave associated with the micro- rotation is predicted to occur in Cosserat solids.
(iv) The range in Poisson's ratio based on stability considerations for an object with free surfaces is from -1 to +0.5, the same as in the classical case.
Articles , mostly experimental
Osteon Article - Strong Cosserat effects seen in the torsion of bone.
Lakes, R. S., "The role of gradient effects in the piezoelectricity of bone", IEEE Trans. Biomed. Eng., BME-27 (5), 282-283, (1980). Stress gradient effects in piezoelectricity are obtained from general nonlocality considerations. A nonlocal elastic and nonlocal piezoelectric continuum representation of bone is appropriate in view of bone's structure. More recently, gradient effects in piezoelectricity have been called "flexoelectricity" of "flexoelectric" materials. Get pdf
J. F. C. Yang and Roderic Lakes, "Transient study of couple stress in compact bone: torsion", Journal of Biomechanical Engineering, 103, 275-279, (1981).
Couple stress theory, which admits an internal moment per unit area as well as the usual force per unit area, is a generalization of classical elasticity. Experimentally we have demonstrated the existence of couple stress by measuring the effect of size on apparent stiffness of compact bone in quasi-static torsion. From these measurements we obtain the characteristic length for bone in couple stress theory. The characteristic length is comparable to the diameter of osteons. Get pdf
Lakes, R. S., "Dynamical study of couple stress effects in human compact bone",
Journal of Biomechanical Engineering, 104, 6-11, (1982).
Torsional resonance experiments performed on wet human compact bone disclose effects due to couple stress. The characteristic length, which is an additional material coefficient which appears in couple stress theory, is of the order of the size of osteons and appears to be smaller at high frequencies than at low frequencies. The presence of couple stress effects implies a reduction in the stress concentration factor around holes, particularly small holes. Get pdf
Yang, J. F. C., and Lakes, R. S., "Experimental study of micropolar and couple stress elasticity in bone in bending", Journal of Biomechanics, 15, 91-98, (1982).
 Generalized continuum theories such as couple stress theory and micropolar theories have degrees of freedom in addition to those of classical elasticity. Such theories are thought to be applicable to materials with a fibrous or granular structure. In this study we observe size effects in quasistatic bending of compact bone. The effects are consistent with micropolar elasticity. From them we evaluate two non-classical elastic constants.Get pdf
Generalized continuum theories such as couple stress theory and micropolar theories have degrees of freedom in addition to those of classical elasticity. Such theories are thought to be applicable to materials with a fibrous or granular structure. In this study we observe size effects in quasistatic bending of compact bone. The effects are consistent with micropolar elasticity. From them we evaluate two non-classical elastic constants.Get pdf
Rod Lakes and Robert Benedict, "
Noncentrosymmetry in micropolar elasticity",
International Journal of Engineering Science, 20 (10), 1161-1167, (1982).
A solid which is isotropic with respect to coordinate rotations but not with respect to inversions is called noncentrosymmetric, acentric, hemitropic, or chiral. Chirality has no effect upon the classical elastic modulus tensor. In Cosserat elasticity, chirality (hemitropy) has an effect. A chiral Cosserat solid has three new elastic constants in addition to the six considered in the fully isotropic micropolar solid. The chiral micropolar solid is predicted to undergo torsional deformation when subjected to tensile load. Thus chiral solids have different mechanical behavior from solids with a center of symmetry, as allowed by the more general Cosserat elastic theory.
doi link
Experimental stretch twist coupling was presented in
R. S. Lakes, Is bone elastically noncentrosymmetric?, Proc. 34th ACEMB. Houston (1981). This is likely the first observation of elastic chirality in a material (in contrast to two ply strips). Get pdf.
Lakes, R. S., "Size effects and micromechanics of a porous solid",
J. Materials Science, 18 2572-2581, (1983).
The rigidity of rods of a polymeric foam in bending and torsion is measured as a function of diameter. The dependence of rigidity upon specimen size is found to be inconsistent with a classically viscoelastic continuum model. The Cosserat continuum, which admits additional degrees of freedom associated with rotation of the microstructure, describes the foam more accurately than the classical continuum. Evidence is presented that additional degrees of freedom, associated with deformation of the microstructure, must be incorporated in a complete continuum model of foamed materials. Specifically a cut off frequency is observed, consistent with the theory of elasticity with microstructure after Mindlin, called micromorphic by Eringen. The material exhibits a stop band of frequency.
Get pdf
Nakamura, S., Benedict, R. L. and Lakes, R. S., "Finite element method for orthotropic micropolar elasticity", International Journal of Engineering Science, 22 319-330 (1984).
The total potential energy for a body composed of an anisotropic micropolar linear elastic material is developed and used to formulate a displacement type finite element method of analysis. As an example of this formulation triangular plane stress (and plane couple stress) elements are used to analyze several problems. The program is verified by computing the stress concentration factor around a hole in an isotropic micropolar material for which an exact analytical solution exists. Several anisotropic material cases are presented which demonstrate the dependence of the stress concentration factor on the micropolar material constants.
doi link,
journal link
Source code, Fortran, as text file. Typical input, input, and output files. No documentation can be provided other than comments already in the code.
Lakes, R. S., "A pathological situation in micropolar elasticity, J. Applied Mechanics, 52 234-235 (1985).
The case of zero coupling number N in micropolar elasticity is considered. This situation has been examined by several investigators to simplify the analysis of micropolar materials. We show that the case N = 0 is pathological and present a physical example. Get pdf
Generalized continuum mechanics of compact bone: a comparison, Cosserat elasticity and the theory of voids, 1985 Advances in Bioengineering, ed. N. Langrana, (1985).
Get pdf
Lakes, R. S., Gorman, D., and Bonfield, W., "Holographic screening method for microelastic solids", J. Materials Science, 20 2882-2888 (1985).
An experimental method is presented for the rapid evaluation of structured solids with microelastic degrees of freedom associated with the microstructure. By contrast with earlier methods based on size effect studies, the present method makes use of holographic interferometry. Results are presented for polymethyl methacrylate (PMMA) and for a dense polyurethane foam, which in previous studies were demonstrated to behave, respectively, as classical elastic and Cosserat solids. The method is based on study of deformation of a square cross section bar, in torsion, with a small crack at the corner. Get pdf.
doi link
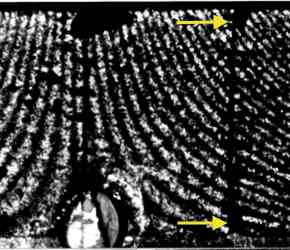
The image on the left shows holographic fringes for a PMMA bar in torsion. The notches at the cross section corner are indicated by yellow arrows. There is no displacement across either notch as indicated by the continuance of fringe order across the notch. This is as expected from classical elasticity.
The image on the left shows holographic fringes for a dense polyurethane foam bar in torsion. The notches at the cross section corner are indicated by yellow arrows. There is a displacement across each notch as indicated by the jump in fringe order across the notch. This is as expected from Cosserat elasticity.

Lakes, R. S., "Demonstration of consequences of the continuum hypothesis", Mechanics Monograph, M5 1-5 (1985).
Get pdf.
The significance of several crucial assumptions within the theory of deformable bodies can be demonstrated via simple observations of motion of a crack in a bar of a structured material. The demonstration is based on a null experiment of a sort requiring no instrumentation. The demonstration is therefore ideally suited for the classroom environment.
Consequences of the continuum hypothesis and its failure may be illustrated by means of a bar of flexible material, of square or rectangular cross section. Such a bar, if sufficiently large, is also useful for demonstrations of principal and anticlastic curvatures in bending, and warp of the cross sections in torsion. For the purposes of this article, consider two such bars, identical in size and shape. Let one be made of rubber and the other of polymeric foam such as that used as packing material.
Consider a differential element at the corner of the bar. The surface traction upon the lateral surface is zero for torsional loading of the bar. By virtue of the symmetry of the stress tensor, the complementary shear stress must be zero. Since all components of the shear stress vanish at the corner, the shear strain must also vanish. By such arguments one can show that the cross sections of a rectangular bar in torsion must undergo warp: see, e.g. F.P. Beer and E.R. Johnston, Jr., Mechanics of Materials, McGraw Hill, New York, 1981. Consider, however, a similar micro-element in a material with a lattice type structure. The struts in the lattice can support a moment as well as a force, as shown in this diagram. The moment must be nonzero since the transverse struts undergo a twist. For the micro-element to be in equilibrium, a nonzero shear force must be transmitted through the longitudinal struts.
The corner elements of an elastic material and a lattice structure, then, are predicted to behave quite differently. To illustrate this difference, make a small nick in the corner of the rubber bar and a similar nick in the corner of the foam bar. When the rubber bar is twisted, the crack is not expected to open in mode III (in which the faces of the crack shear parallel to each other and parallel to the crack front) since there is no stress in the region of the crack. While this is strictly true only for an infinitesimal crack, the crack opening is negligibly small if the crack is sufficiently short compared with the bar width, as shown in as shown in figure 3. The situation is different in the foam bar shown in figure 4. The corner crack opens noticeably in mode III when the bar is twisted. Here the corner of the bar has been made more visible by gluing black thread to it with rubber cement. A line can also be drawn with ink as was done with the rubber bar, but the line tends to be rather broad, due to the structure of the foam. The continuum view is shown in figure 5
Lakes, R. S., "Experimental microelasticity of two porous solids",
International Journal of Solids and Structures, 22 55-63 (1986).
doi link

Experiments are performed to determine the dependence of torsional and bending rigidity upon diameter for rod-shaped specimens of dense polyurethane foam and of syntactic foam. Results show an effect due to the microstructure. Size effects are observed in the linear regime of small strain. Results are describable by a Cosserat elastic model. All six Cosserat elastic constants are determined from experiment.
Get pdf of this article.
 Lakes, R. S. and Saha, S., "Cement line motion in bone," Science, 204,
501-503 (1979). Get pdf.
Lakes, R. S. and Saha, S., "Cement line motion in bone," Science, 204,
501-503 (1979). Get pdf.
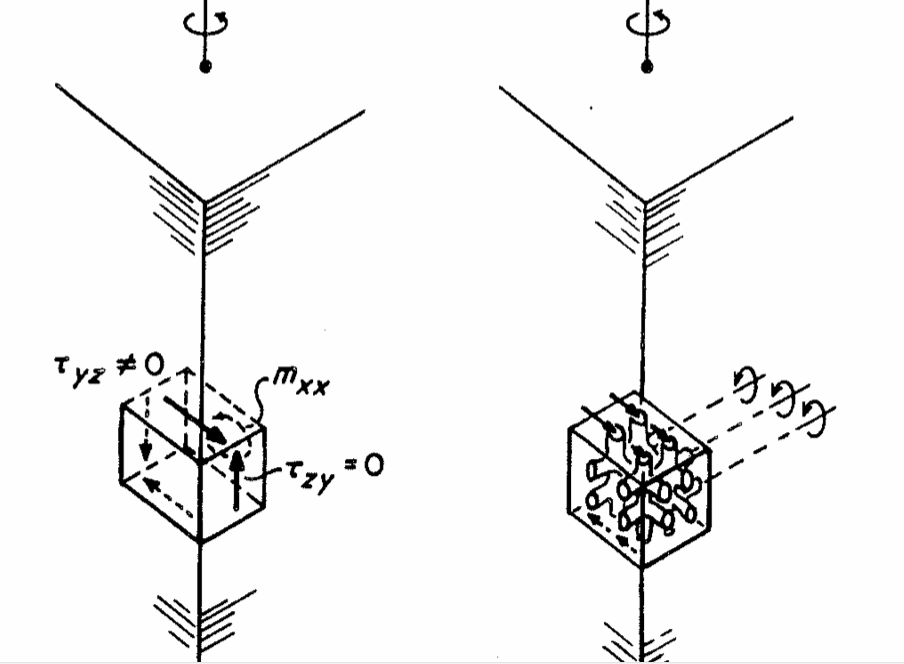
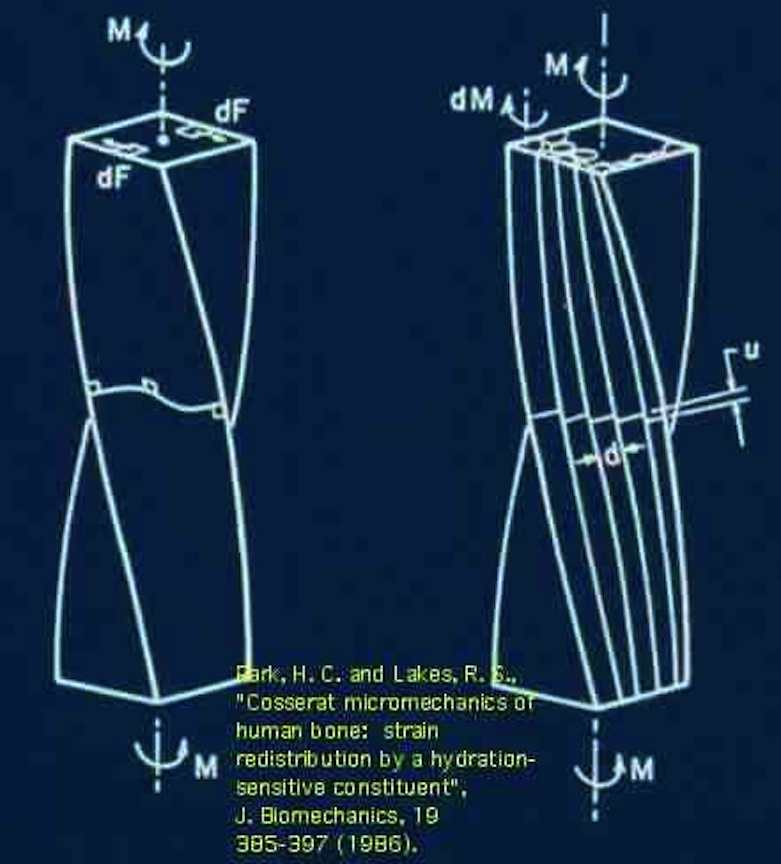
Motion at the cement lines occurs in bone under prolonged load. Such motion is considered responsible for the long term creep in bone. The diagram at the right shows the interpretation of heterogeneous deformation in the context of Cosserat elasticity.
Park, H. C. and Lakes, R. S., "Cosserat micromechanics of human bone: strain redistribution by a hydration-sensitive constituent", J. Biomechanics, 19 385-397 (1986). The diagram at the right shows the interpretation of reduction of warp in the context of Cosserat elasticity.
Experimental mechanics determination of the strain distribution in prismatic, square cross section bars of human compact bone in torsion disclosed nonclassical effects associated with the microstructure. Specifically, in wet bone at small strain, significant deviations from the classically predicted strain distribution were observed. The measured strain distribution in wet bone followed predictions based on Cosserat (micropolar) elasticity. Predictive power of Cosserat elasticity is illustrated by the fact the correct
strain distribution is predicted assuming the characteristic lengths obtained from size effect studies. In dry bone, the strain distribution was very close to the prediction of classical elasticity. The interaction between Haversian osteons and the cement substance between them was hypothesized to be the principal mechanism for the phenomena. To evaluate this hypothesis, additional specimens were subjected to prolonged torsional load and the cement lines were observed by reflected light microscopy. Localized deformation at the cement lines was observed, but it was less than values reported earlier for bovine plexiform bone.
Get pdf.
Park, H. C. and Lakes, R. S. "Torsion of a micropolar elastic prism of square cross section", Int. J. Solids, Structures, 23, 485-503 (1987).
An analytical solution is presented for the problem of torsion of a prismatical bar of square cross section of a micropolar (Cosserat) elastic solid. Warp of the cross sections is found to differ from the warp in a classically elastic solid. Contrary to the classical case, a nonzero shear strain is predicted to occur at the edge of the bar. Novel experimental modalities are suggested on the basis of this analytical solution. The strain distribution across the lateral surfaces depends on the Cosserat characteristic length as shown in this diagram Download pdf.
doi link
Lakes, R. S., "Negative Poisson's ratio materials", Science, 238 551 (1987).
In the Cosserat model for structured solids, many phenomena are predicted and observed that depend on the material size scale in relation to the length scale associated with the deformation. A simple tension deformation (in an isotropic material) however is uniform and has no associated length scale. Consequently both the Cosserat model and classical elasticity predict the Poisson effect to be independent of scale. As for causes, structural aspects may be responsible both for Cosserat effects and negative Poisson's ratio.
Get
pdf or gif from here.
Top
Nakamura, S. and Lakes, R. S. "Finite element analysis of stress concentration around a blunt crack in a Cosserat elastic solid", Computer Methods in Applied Mechanics and Engineering, 66, 257-266 (1988).
The problem of a blunt edge notch of elliptic contour in a strip of Cosserat (micropolar) elastic material under tension has been analyzed via two-dimensional (plane stress) finite element analysis. Both 3-node constant strain triangular elements and 4-node isoparametric elements were used. Three cases were explored: Cosserat characteristic length much less than the crack root radius, equal to the crack root radius; and comparable to the crack length. Stress concentration factors were found to be reduced by as much as a factor of 2.6 in comparison with a classically elastic material. For the special case of a classically elastic material, the finite element results agreed well with the classical analytic solution. Get pdf.
Chen, C. P. and Lakes, R. S., "Dynamic wave dispersion and loss properties of conventional and negative Poisson's ratio polymeric cellular materials", Cellular Polymers, 8(5), 343-359 (1989).
This article describes experimental investigations of the dynamical behaviour of conventional and negative Poisson's ratio foamed materials in torsional vibration. Dispersion of standing waves and cut-off frequencies were observed. Consequently, foamed materials do not obey the classical theory of elasticity or viscoelasticity. The dynamical effects were attributed to micro-vibrations of the cell ribs in a structural view and were associated with Mindlin microstructure elasticity or micromorphic elasticity in a continuum view. Cut-off frequencies were lower in re-entrant foams with negative Poisson's ratios than in the conventional foams from which they were derived. An analytical structural model was developed in which the ribs of the conventional foams were modeled as free-free vibrating beams. The predicted cut-off frequencies were comparable to those observed experimentally. Such stop bands can block waves.
Get pdf
Lakes, R. S., Nakamura, S., Behiri, J. C. and Bonfield, W., "Fracture mechanics of bone with short cracks", Journal of Biomechanics, 23, 967-975 (1990).
Tensile fracture experiments were performed upon specimens of wet mature bovine Haversian bone, with short, controlled notches. Stress concentration factors were found to be significantly less than values predicted using a maximum stress criterion in the theory of elasticity. Results were also modeled with the aid of linear elastic fracture mechanics. Agreement of experiment with theory was better in this case, however deviations were seen for short notches. Two mechanisms were evaluated for the behavior: plasticity near the crack tip, and effects of the Haversian microstructure, modelled by Cosserat elasticity, a generalized continuum theory. Plastic zone effects were found to be insignificant. Cosserat elasticity, by contrast, predicted stress concentration factors which better approximated observed values. To explore strain redistribution processes, further experiments were conducted upon notched specimens in torsion at small strain. They disclosed a strain redistribution effect consistent with Cosserat elasticity. These microelastic effects interpreted within a micropolar continuum model, are attributed to the Haversian architecture of bone. Get pdf.
Lakes, R. S., "Experimental micro mechanics methods for conventional and negative Poisson's ratio cellular solids as Cosserat continua", J. Engineering Materials and Technology, 113, 148-155 (1991).
 Continuum representations of micromechanical phenomena in structured materials are described, with emphasis on cellular solids. These phenomena are interpreted in light of Cosserat elasticity, a generalized continuum theory which admits degrees of freedom not present in classical elasticity. These are the rotation of points in the material, and a couple per unit area or couple stress. Experimental work in this area is reviewed, and other interpretation schemes are discussed. The applicability of Cosserat or micropolar elasticity to cellular solids and fibrous composite materials is considered as is the application of related generalized continuum theories. New experimental results are presented for foam materials with negative Poisson's ratios.
Get pdf
Continuum representations of micromechanical phenomena in structured materials are described, with emphasis on cellular solids. These phenomena are interpreted in light of Cosserat elasticity, a generalized continuum theory which admits degrees of freedom not present in classical elasticity. These are the rotation of points in the material, and a couple per unit area or couple stress. Experimental work in this area is reviewed, and other interpretation schemes are discussed. The applicability of Cosserat or micropolar elasticity to cellular solids and fibrous composite materials is considered as is the application of related generalized continuum theories. New experimental results are presented for foam materials with negative Poisson's ratios.
Get pdf
A heavily twisted bar of negative Poisson's ratio foam exhibits minimal warp, in contrast to expectation of classical elasticity as shown in the image.
Chen, C. P. and Lakes, R. S., "Holographic study of conventional and negative Poisson's ratio metallic foams: elasticity, yield, and micro-deformation", J. Materials Science, 26, 5397-5402 (1991)
This article presents an experimental study by holographic interferometry of the following material properties of conventional and negative Poisson's ratio copper foams: Young's moduli, Poisson's ratios, yield strengths, and characteristic lengths associated with inhomogeneous deformation. The Young's modulus and yield strength of the conventional copper foam were comparable to those predicted by microstructural modelling on the basis of cellular rib bending. The re-entrant copper foam exhibited a negative Poisson's ratio as indicated by the elliptic contour fringes on the specimen surface in the bending tests. Inhomogeneous, non-affine deformation was observed holographically in both foam materials.
Get pdf
Lakes, R. S., "Strongly Cosserat elastic lattice and foam materials for
enhanced toughness", Cellular Polymers, 12, 17-30 (1993).
Some foams exhibit size effects and other phenomena not describable by classical elasticity. These foams are describable by Cosserat elasticity, which is a continuum theory with more freedom than classical elasticity. Cosserat solids have a characteristic length which is greater than zero. Strongly Cosserat elastic materials are considered to be those materials for which the Cosserat characteristic length is substantially greater than the structure size and for which the coupling number is large. Such materials are predicted to exhibit superior toughness. A mechanically isotropic lattice model is presented for the study of foams. Ordinary open cell foams are shown to be weakly Cosserat elastic. If cell rib properties are modified, strongly Cosserat elastic effects can occur in the foam. Anisotropic laminate and fibrous materials can also be made to exhibit strongly Cosserat elastic effects.
Get pdf
Chen, C. P. and Lakes, R. S., "Holographic study of non-affine deformation in copper foam with a negative Poisson's ratio -0.8", Scripta Metall et Mater., 29, 395-399, (1993).
Micro-deformation studies of conventional and negative Poisson's ratio copper foams were conducted holographically. Inhomogeneous, non-affine deformation was observed holographically in both foam materials. The negative Poisson's ratio material with a permanent volumetric compression ratio 2.2 exhibited a substantially greater non-affine deformation than the conventional material, in contrast to foam with compression ratio 3.0 examined earlier.
Get pdf
Anderson, W. B., Chen, C. P., and Lakes, R. S., "Experimental study of size effects and surface damage of polymethacrylimide closed-cell foam", Cellular Polymers, 13, 1-15 (1994).
Get pdf
Anderson, W. B. and Lakes, R. S., "Size effects due to Cosserat elasticity and surface damage in closed-cell polymethacrylimide foam", Journal of Materials Science, 29, 6413-6419, (1994).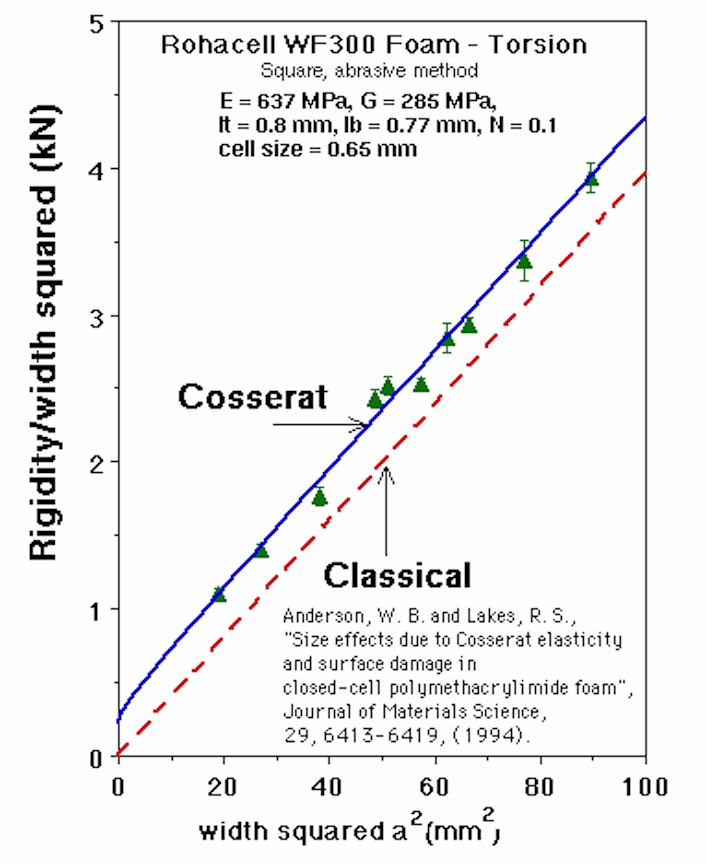
This article describes the experimental investigation of Cosserat (or micropolar) elasticity and surface damage effects in closed cell polymethacrylimide foams of different densities. The method of size effects was used to find the degree of Cosserat behavior for both cylindrical and square cross section specimens in bending and torsion. The foams were found to behave as Cosserat materials (slender specimens appear less stiff than thick ones), provided sufficient care is taken when machining the specimens. Surface damage caused by the machining process may cause the apparent stiffness to decrease with decreasing specimen size, giving an opposite softening size effect.
Get pdf
Anderson, W. B., Lakes, R. S., and Smith, M. C., "Holographic evaluation of warp in the torsion of a bar of cellular solid", Cellular Polymers, 14, 1-13, (1995).
Holographic interferometry methods are utilized to examine deviations from classical elasticity in a cellular solid, polymethacrylamide closed cell foam. A square cross section bar is subjected to static torsional deformation. The warp deformation is observed to be less in a foam bar than in a homogeneous polymeric bar used as a control. The homogeneous bar obeys the predictions of classical elasticity. Behavior of the foam bar is consistent with Cosserat elasticity. In a Cosserat solid, points in the continuum to rotate as well as translate, and the material supports couple per unit area as well as force per unit area. Cosserat effects can lead to enhanced toughness even in all brittle composites since stress concentrations are reduced. The image on the right shows holographic fringes associated with warp. This image shows computer generated fringe patterns associated with warp. The degree of warp depends on the Cosserat elastic constants. Get pdf
This image shows computer generated fringe patterns associated with warp. The degree of warp depends on the Cosserat elastic constants. Get pdf
Cellular solids are two phase composite materials in which one phase is solid and the other is a fluid, most often air. If the size scale becomes large enough, the material may no longer be assumed to be continuous. Some researchers have found that classical elasticity theory does not always adequately describe the behavior of cellular materials. In composite materials with stress concentrations due to holes or cracks, the observed fracture behavior is not correctly predicted by the classical theory of anisotropic elasticity. The experimental stress concentrations are consistently less than the theoretical ones [1]. The non-classical fracture behavior has been dealt with using point stress and average stress criteria, however that approach cannot account for non-classical strain distributions in objects under small load. Strain distributions have been observed in fibrous composites and cellular solids which differ from the predictions of classical elasticity, particularly near small holes and small cracks. Observed concentrations of strain are less than predicted values. Strain fields around large holes, by contrast, follow classical predictions. A more general continuum theory such as Cosserat elasticity (micropolar continuum theory) or nonlocal elasticity, may be of use in predicting non-classical strain distributions. In this study, size effects in the mechanical rigidity of foams are examined experimentally. Analysis of the results is via generalized continuum mechanics and a model of surface damage.
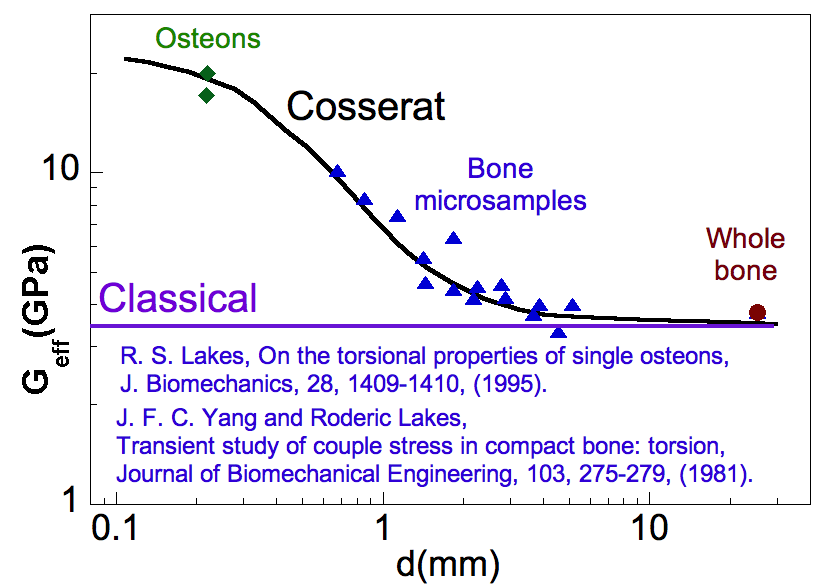
Lakes, R. S., "On the torsional properties of single
osteons", J. Biomechanics, 28, 1409-1410, (1995). The high effective shear moduli of osteons that was observed by Ascenzi et. al. (1994) is interpreted in the context of size effects previously observed in bone. These phenomena are analyzed in the context of Cosserat elasticity.
Lakes, R. S., "Experimental methods for study of Cosserat elastic solids
and other generalized continua", in Continuum models for materials with micro-structure, ed. H. Mühlhaus, J. Wiley, N. Y. Ch. 1, p. 1-22, (1995).
The behavior of solids can be represented by a variety of continuum theories. For example, Cosserat elasticity allows the points in the continuum to rotate as well as translate, and the continuum supports couple per unit area as well as force per unit area. We examine experimental methods for determining the six Cosserat elastic constants of an isotropic elastic solid, or the six Cosserat relaxation functions of a Cosserat viscoelastic solid. We also consider other generalized continuum theories (including micromorphic elasticity in which points rotate and deform, Cowin's void theory (theory of voids) in which the points dilate, and nonlocal elasticity). Ways of experimentally discriminating among various generalized continuum representations are presented. The applicability of Cosserat elasticity to cellular solids and fibrous composite materials is considered as is the application of related generalized continuum theories.
Get pdf of this review article.
Nakamura, S. and Lakes, R. S., "Finite element analysis of Saint Venant end effects in micropolar elastic solids", Engineering Computations, 12, 571-587, (1995).
Distributions of stress and strain in composite and cellular materials can differ significantly from the predictions of classical elasticity. For example, concentration of stress and strain around holes and cracks is consistently less than classical predictions. Generalized continuum theories such as micropolar (Cosserat) elasticity offer improved predictive power. In this article Saint-Venant end effects for self equilibrated external forces in micropolar solids are investigated in two dimensions. A two dimensional finite element analysis is used which takes into account the extra degrees of freedom, to treat the problem of localized end loads acting upon a strip. The rate of decay of strain energy becomes slower in a two dimensional strip as the micropolar characteristic length l is increased (for l sufficiently less than the strip width). For the strip geometry a Cosserat solid exhibits slower stress decay than a classical solid.
Get pdf
Prall, D. and Lakes, R. S., "Properties of a chiral honeycomb with a Poisson's ratio of -1", Int. J. of Mechanical Sciences, 39, 305-314, (1997).
 A theoretical and experimental investigation is conducted of a two-dimensionally chiral honeycomb. The honeycomb exhibits a Poisson's ratio of -1 for deformations in-plane. This Poisson's ratio is maintained over a significant range of strain, in contrast to the variation with strain seen in known negative Poisson's ratio materials. This is the first two-dimensional lattice metamaterial that is chiral; we did not call it by such a name.
Remark: these chiral honeycombs, also called chiral lattices, have been analyzed as Cosserat elastic solids.
A theoretical and experimental investigation is conducted of a two-dimensionally chiral honeycomb. The honeycomb exhibits a Poisson's ratio of -1 for deformations in-plane. This Poisson's ratio is maintained over a significant range of strain, in contrast to the variation with strain seen in known negative Poisson's ratio materials. This is the first two-dimensional lattice metamaterial that is chiral; we did not call it by such a name.
Remark: these chiral honeycombs, also called chiral lattices, have been analyzed as Cosserat elastic solids.
A. Spadoni, M. Ruzzene, Elasto-static micropolar behavior of a chiral auxetic lattice, Journal of the Mechanics and Physics of Solids, 60, 156-171 (2012).
X. N. Liu, G. L. Huang, G. K. Hu, Chiral effect in plane isotropic micropolar elasticity and its application to chiral lattices, Journal of the Mechanics and Physics of Solids, 60, 1907-1921 (2012).
Lakes, R. S., "Elastic freedom in cellular solids and composite materials", in Mathematics of Multiscale Materials, p. 129-153, ed. K. Golden, G. Grimmert, R. James, G. Milton, P. Sen, IMA vol. 99, Springer, NY, Berlin, (1998). The question of how much freedom is to be incorporated in a continuum theory must ultimately be decided by experiment. There are several theories which describe behavior of materials. An early uniconstant theory was proposed based on atomic interaction theory; it was abandoned since it predicted a Poisson's ratio of 1/4 for all materials. The elasticity theory currently accepted as classical allows Poisson's ratios in isotropic materials in the range -1 to 1/2. Common materials exhibit a Poisson's ratio from 1/4 to nearly 1/2. We have prepared materials with a Poisson's ratio as small as -0.8. Deformation mechanisms in these materials include relative rotation of micro-elements, and non-affine micro-deformation. The relation between properties and structure is exploited to prepare viscoelastic composites with high stiffness combined with high damping. Generalized continuum theories exist with more freedom than classical theory. For example, in Cosserat elasticity there are characteristic lengths as additional engineering elastic constants. Recent experimental work discloses a variety of cellular and fibrous materials to exhibit such freedom, and the characteristic lengths have been measured. In hierarchical solids structural elements themselves have structure. Several examples of natural structural hierarchy are considered, with consequences related to optimality of material properties.
Get pdf
Lakes, R. S., "Elastic and viscoelastic behaviour of chiral materials", Int. J. of Mechanical Sciences, 43, 1579-1589, June (2001).
Chiral materials are not invariant to inversions: there is a distinction between right and left handed material. Material properties such as piezoelectricity and pyroelectricity, represented by tensors of odd rank, can only occur in chiral materials. Chiral effects in elasticity cannot be expressed within classical elasticity since the modulus tensor, which is fourth rank, is unchanged under an inversion. We consider effects of chirality in elastic materials described by a generalized continuum representation, specifically Cosserat elasticity. Analysis of several configurations discloses a chiral material to generate reaction moments when compressed as a slab. A chiral plate bent to hyperbolic shape is predicted to exhibit size effects from the Cosserat characteristic length, and a shear force from the chirality. This analysis can be used for the interpretation of experiments on compliant chiral materials, in particular the evaluation of the elastic constants. Viscoelastic chiral solids are examined in the context of the correspondence principle.
Download pdf .
Buechner, P. M., and Lakes, R. S., "Size effects in the elasticity and viscoelasticity of bone", Biomechanics and Modeling in Mechanobiology, 1 (4), 295-301 (2003). Size effects of large magnitude are observed in the torsional shear modulus and damping of bovine plexiform bone. Damping increases and stiffness decreases with specimen size over all sizes studied. Measurements were conducted in torsion using a laser based micromechanics apparatus capable of viscoelastic studies over a range of frequencies up to 100 kHz, upon samples of various size, with no parasitic friction or other errors that could mimic any size effect. Torsional tan delta at 1 Hz varies by about a factor of five over the size range 2.8 to 6.2 mm thick, and is more dependent on specimen thickness at 1 Hz than it is at higher frequency. The size effects are attributed to compliance and viscoelasticity of the interfaces between laminae. These laminae must be substantially stiffer than whole bone. Observed size effects are likely to play a role in understanding scaling laws of bones in living organisms.
Get pdf
Top
Lakes, R. S., Third-rank piezoelectricity in isotropic chiral solids, Appl. Phys. Lett., 106, 212905, May (2015).
The highest symmetry in which piezoelectricity was thought to occur is cubic. Here, it is shown that third rank piezoelectricity can occur in isotropic chiral solids. Polarization is coupled via an isotropic third rank tensor to the antisymmetric part of the stress. Asymmetric stress can occur if balanced by moments distributed over area or volume. Such moments occur in heterogeneous solids, in which there exists a characteristic length associated with the microstructure: the Cosserat or micropolar solids. Effects associated with nonzero structure size are predicted, including radial polarization in response to torsion. These effects do not occur in gradient type flexoelectric materials; they are governed by a different tensorial rank and symmetry.
DOI: 10.1063/1.4921846
journal link
Get preprint pdf
Lakes, R. S. and Drugan, W. J., "Bending of a Cosserat elastic bar of square cross section - theory and experiment", Journal of Applied Mechanics, 82(9), 091002 (2015). (8 pages).
Pure bending experiments on prismatic bars of square cross-section composed of reticulated polymer foam exhibit deformation behavior not captured by classical elasticity theory. Sigmoidal deformation of the bars' lateral surfaces is observed. The surfaces are predicted by classical elasticity theory to tilt but remain planar upon application of pure moments to the ends. An approximate Cosserat three-dimensional solution to pure bending is obtained. This solution captures the experimentally-observed nonclassical deformation.
preprint;
journal reprint link.
Ha, C. S., Plesha, M. E., Lakes, R. S., "Chiral three dimensional lattices with tunable Poisson's ratio", Smart Materials and Structures, 25, 054005 (6pp) (2016).
Chiral three dimensional cubic lattices are developed with rigid cubical nodules and analyzed via finite element analysis. The lattices exhibit geometry dependent Poisson's ratio that can be tuned to negative values. Poisson's ratio tends to zero as the cubes become further apart. The lattices exhibit stretch twist coupling. Such coupling cannot occur in a classical elastic continuum but it can occur in a chiral Cosserat solid.
journal link.
preprint pdf
Rueger, Z. and Lakes, R. S., "Cosserat elasticity of negative Poisson's ratio foam: experiment", Smart Materials and Structures, 25 054004 (8pp) (2016).
Negative Poisson's ratio polymer foams derived from reticulated open cell foams exhibit large size effects in torsion and bending. Effective moduli increase as diameter decreases in contrast to the prediction of classical elasticity. Size effects of this sort are predicted by Cosserat (micropolar) elasticity in which points can rotate as well as translate and distributed moments are incorporated. The Cosserat coupling number N was about twice as large as that of as-received foam, leading to strong effects. The torsion characteristic length was similar. Cosserat effects are known to enhance toughness and immunity from stress concentration.
journal preprint link.
preprint pdf
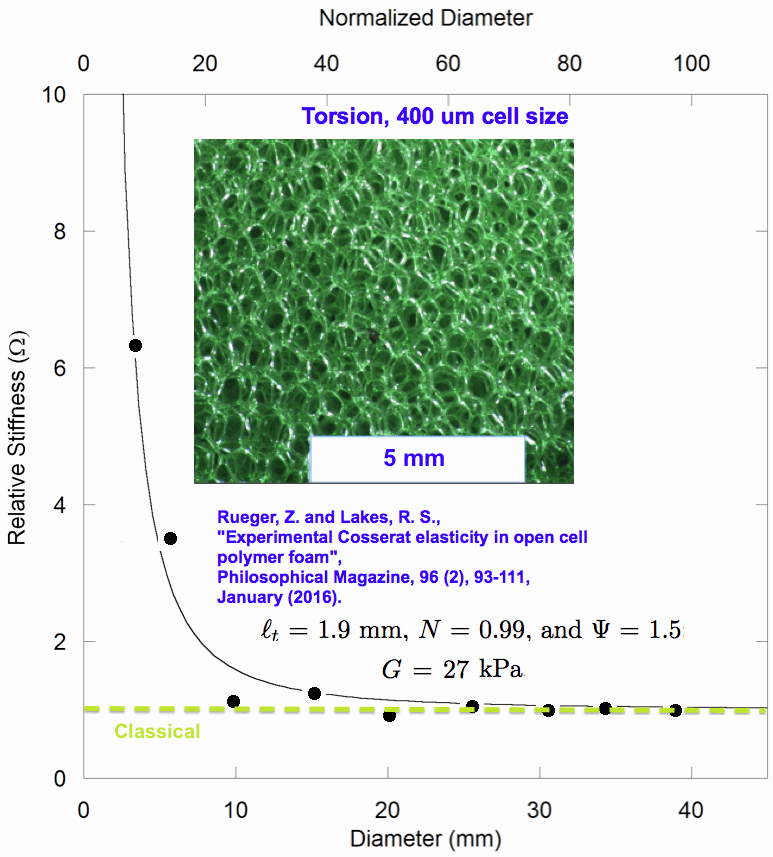 Rueger, Z. and Lakes, R. S., "Experimental Cosserat elasticity in open cell polymer foam", Philosophical Magazine, 96 (2), 93-111, January (2016).
Reticulated open-cell polymer foams exhibit substantial size effects in torsion and bending: slender specimens are more rigid than anticipated via classical elasticity. Such size effects are predicted by Cosserat (micropolar) elasticity, which allows points to rotate as well as translate and incorporates distributed moments (couple stresses). The Cosserat characteristic length is larger than the cell size. The Cosserat coupling coefficient is larger than in dense closed-cell foams and approaches 1 for foam with 0.4 mm cells.
Rueger, Z. and Lakes, R. S., "Experimental Cosserat elasticity in open cell polymer foam", Philosophical Magazine, 96 (2), 93-111, January (2016).
Reticulated open-cell polymer foams exhibit substantial size effects in torsion and bending: slender specimens are more rigid than anticipated via classical elasticity. Such size effects are predicted by Cosserat (micropolar) elasticity, which allows points to rotate as well as translate and incorporates distributed moments (couple stresses). The Cosserat characteristic length is larger than the cell size. The Cosserat coupling coefficient is larger than in dense closed-cell foams and approaches 1 for foam with 0.4 mm cells.
journal link.
preprint pdf
Lakes, R. S., "Static and dynamic effects of chirality in dielectric media", Modern Physics Letters B, 30 (24) 1650319 (9 pages) (2016).
Chiral dielectrics are considered from the perspective of continuum representations of spatial heterogeneity. Static effects in isotropic chiral dielectrics are predicted, provided the electric field has nonzero third spatial derivatives. The effects are compared with static chiral phenomena in Cosserat elastic materials which obey generalized continuum constitutive equations. Dynamic monopole-like magnetic induction is predicted in chiral dielectric media.
preprint pdf
Lakes, R. S., "Physical meaning of elastic constants in Cosserat, void, and microstretch elasticity", Journal of Mechanics of Materials and Structures, 11 (3), 217-229 (2016).
The physical meaning of Cosserat, void, and microstretch elastic constants is analyzed and interpreted. Various torsion experiment designs provide a clear path to extract Cosserat elastic constants independently of any dilatation gradient sensitivity the material may have. For void elasticity (with sensitivity to dilatation gradients) there is no known quasistatic modality to demonstrate phenomena or extract elastic constants independently of any sensitivity to rotation gradients. Wave methods may be appropriate if there is minimal viscoelastic dispersion. Microstretch elasticity, which includes sensitivity to gradients of rotation and of dilatation could account for bending effects larger than those of Cosserat elasticity.
journal link.
preprint pdf
Lakes, R. S., "Reduced warp in torsion of reticulated foam due to Cosserat elasticity: experiment", Zeitschrift fuer Angewandte Mathematik und Physik (ZAMP), 67(3), 1-6 (2016).
Warp of cross sections of square section bars in torsion is reduced in Cosserat elasticity in comparison with classical elasticity. Warp is observed experimentally to be substantially reduced, by about a factor of four compared with classical elasticity, in an open cell polymer foam for which Cosserat elastic constants were previously determined. The observed warp in the foam is consistent with a prediction based on Cosserat elasticity. Concentration of strain in the foam is therefore reduced in comparison with classical elasticity.
journal link.
preprint pdf
 Ha, C. S., Plesha, M. E., Lakes, R. S., "Chiral three-dimensional isotropic lattices with negative Poisson's ratio", Physica Status Solidi B, 253, (7), 1243-1251 (2016).
DOI: 10.1002/pssb.201600055
Ha, C. S., Plesha, M. E., Lakes, R. S., "Chiral three-dimensional isotropic lattices with negative Poisson's ratio", Physica Status Solidi B, 253, (7), 1243-1251 (2016).
DOI: 10.1002/pssb.201600055
Chiral three-dimensional isotropic cubic lattices with rigid cubical nodules and multiple deformable ribs are developed and analyzed via finite element analysis. The lattices exhibit geometry dependent Poisson's ratio that can be tuned to negative values. Poisson's ratio decreases from positive to negative values as the number of cells increases. Isotropy is obtained by adjustment of aspect ratio. The lattices exhibit significant size effects. Such a phenomenon cannot occur in a classical elastic continuum but it can occur in a Cosserat solid. The material exhibits squeeze-twist coupling and stretch-twist coupling.
This is the first three-dimensional metamaterial that is chiral; we did not call it by such a name.
journal link. Figure on cover link
preprint pdf
Rueger, Z. and Lakes, R. S., "Strong Cosserat elastic effects in a unidirectional composite", Zeitschrift fuer Angewandte Mathematik und Physik (ZAMP), 68(54) 9 pages (2017). https://doi.org/10.1007/s00033-017-0796-6
Strong Cosserat elastic effects are observed in a designed composite consisting of unidirectional corrugated tubes in a hexagonal array. The torsional characteristic length is much larger than the tube diameter. The effective coupling number N approaches its upper bound of 1. Extremely large size effects are observed, about a factor of 128 in torsion.
journal link,
reprint link
preprint pdf
Rueger, Z., Li, D., Lakes, R. S., "Observation of Cosserat elastic effects in a tetragonal negative Poisson's ratio lattice" Physica Status Solidi B, 254, (12), 1600840, 6 pages, Dec. (2017).
Size effects are explored experimentally in a tetragonal lattice structure. Size dependence of rigidity is nonclassical elastic and is interpreted via Cosserat elasticity. The characteristic lengths are about a third the cell size. The size effect in torsion was a factor 4.5 in rigidity. The ratio of characteristic length to cell size is larger than in fully stretch dominated lattices but smaller than in bend dominated honeycombs or foams.
These may be called truss metamaterials.
journal link
http://onlinelibrary.wiley.com/store/10.1002/pssb.201600840/asset/pssb201600840.pdf?v=1&t=jb6z76od&s=0752c7ff89687201970bd9dd4717eb5034212ff2
preprint pdf
Drugan, W. J. and Lakes, R. S., "Torsion of a Cosserat elastic bar with square cross section: theory and experiment", Zeitschrift fur angewandte Mathematik und Physik (ZAMP), 69(2), 24 pages (2018).
An approximate analytical solution for the displacement and microrotation vector fields is derived for pure torsion of a prismatic bar with square cross section comprised of homogeneous, isotropic linear Cosserat elastic material. This is accomplished by analytical simplification coupled with use of the principle of minimum potential energy together with polynomial representations for the desired field components. Explicit approximate expressions are derived for cross section warp and for applied torque versus angle of twist of the bar. These show that torsional rigidity exceeds the classical elasticity value, the difference being larger for slender bars, and that cross section warp is less than the classical amount. Experimental measurements on two sets of 3D printed square cross section polymeric bars, each set having a different microstructure and four different cross section sizes, revealed size effects not captured by classical elasticity but consistent with the present analysis for physically sensible values of the Cosserat moduli. The warp can allow inference of Cosserat elastic constants independently of any sensitivity the material may have to dilatation gradients; warp also facilitates inference of Cosserat constants that are difficult to obtain via size effects.
journal link. https://doi.org/10.1007/s00033-018-0913-1
preprint
Lakes, R. S., "Stability of Cosserat solids: size effects, ellipticity and waves", Journal of mechanics of materials and structures (JoMMS), 13 (1) 83-91 (2018).
We consider stability in Cosserat solids. To obtain restrictions on elastic constants based on positive definite strain energy, energy terms are tacitly assumed to be independent. In finite-size objects, however, the terms are linked in Cosserat materials. Therefore, in contrast to classical solids, the stability of Cosserat solids appears to depend on the size and shape of the specimen, provided strong ellipticity is satisfied. Stability in the presence of stored energy is possible. Solids with microstructure and stored energy offer the potential to facilitate attainment of extreme behavior in the presence of spatial gradients. Snap- through buckling in torsion is envisaged by analogy to the axial buckling concept used for composites with negative stiffness inclusions. It is possible to support compressive load in a stable manner but to dissipate energy in the presence of spatial gradients as in torsion or bending.
journal link
preprint pdf
DOI: 10.2140/jomms.2018.13.83
Andrade, C., Ha, C. S., Lakes, R. S., "Extreme Cosserat elastic cube structure with large magnitude of negative Poisson's ratio", Journal of mechanics of materials and structures (JoMMS), 13 (1) 93-101 (2018).
A structure consisting of pivoting cubes is presented. It has zero Young's modulus and zero bulk modulus. Poisson's ratio has large negative values in all directions; the structure exhibits anisotropy in Poisson's ratio. The structure is compliant in tension but rigid in torsion and bending. The Cosserat characteristic length tends to infinity.

preprint pdf
journal link DOI: 10.2140/jomms.2018.13.93
Rueger, Z. and Lakes, R. S., "Strong Cosserat elasticity in a transversely isotropic polymer lattice", Physical Review Letters, 120, 065501 Feb. (2018).
Large size effects are experimentally measured in lattices of triangular unit cells: about a factor of 36 in torsion rigidity and 29 in bending rigidity. This nonclassical phenomenon is consistent with Cosserat elasticity which allows for rotation of points and distributed moments in addition to the translation of points and force stress of classical elasticity. The Cosserat characteristic length for torsion is 9.4 mm; for bending it is 8.8 mm; these values are comparable to the cell size. Nonclassical effects are much stronger than in stretch dominated lattices with uniform straight ribs. The lattice structure provides a path to attainment of arbitrarily large effects.
journal reprint link; get pdf.
Some may call these metamaterials.
Rueger, Z., Ha, C. S. and Lakes, R. S., "Flexible cube tilt lattice with anisotropic Cosserat effects and negative Poisson's ratio" Physica Status Solidi B, 256, 1800512 (2019).
A 3D lattice structure consisting of pivoting cubes with flexible links at the corners is presented. It exhibits anisotropic negative Poisson's ratio -0.54 and -0.75. Size effects occur in torsion and bending; these effects are consistent with Cosserat elasticity but not with classical elasticity. Cosserat elastic solids exhibit sensitivity to strain gradients; size effects occur in torsion and bending; also reduction in stress concentrations. The Cosserat effects also reveal anisotropy.

doi.org/10.1002/pssb.201800512 link; journal link
preprint pdf
Rueger, Z. and Lakes, R. S., "Experimental study of elastic constants of a dense foam with weak Cosserat coupling", J. Elasticity, 137(1), 101-115, (2019).
A dense closed cell foam is studied to determine which continuum theory of elasticity is applicable. Size effects inconsistent with classical elasticity are observed. The material exhibits a characteristic length scale considerably larger, by more than a factor 6, than the largest observable structure size. The Cosserat coupling number N is shown to be small, via measurements of size effects in square section bars, comparison with size effects in round section bars, and determination of warp of a square section bar in torsion. For this material, the couple stress theory is excluded and the modified couple stress theory is excluded. Theories that force constants to their thermodynamic limits do not apply to this foam. The role of other generalized continuum theories is considered.
https://doi.org/10.1007/s10659-018-09714-8 link
Journal link
preprint pdf
Z. Rueger, C. S. Ha and R. S. Lakes, "Cosserat elastic lattices", Meccanica, 54(13), 1983-1999, (2019).
Lattices composed of cubic and triangular prismatic unit cells with polymeric Sarrus linkage rib elements are designed, fabricated via 3D printing and studied experimentally. Size effects in these lattices are observed experimentally; slender specimens appear more rigid in torsion and in bending than expected via classical elasticity. Effects are analyzed via Cosserat elasticity. The magnitude of size effects is sensitive to geometry of the lattices; triangular cells with short ribs revealed the most extreme effects, also the largest characteristic length in relation to cell size. The torsion coupling number is 1, its upper bound, for all lattices. A path to the attainment of arbitrarily large nonclassical effects is delineated.
These may be called truss metamaterials.
preprint pdf
DOI 10.1007/s11012-019-00968-7 link
journal link
journal link 2
D. Reasa and R. S. Lakes, "Cosserat effects in achiral and chiral cubic lattices", Journal of Applied Mechanics (JAM), 86, 111009-1, 6 pages Nov. (2019).
Cubic 3D lattices were designed, made by 3D printing, and studied experimentally. One lattice was simple cubic with ribs of diameter 1/5 the cell size. The second lattice was chiral, with spiral ribs. The chiral lattice, but not the achiral lattice, exhibited squeeze-twist coupling with size effects. Squeeze-twist coupling cannot occur in a classically elastic solid but is anticipated by theory in a Cosserat solid. Both lattices exhibited size effects in bending and torsion.
These may be called truss metamaterials.
DOI link https://doi.org/10.1115/1.4044047
preprint pdf
J. Li, C. S. Ha, R. S. Lakes, "Observation of squeeze twist coupling in a chiral three-dimensional isotropic lattice", Physica Status Solidi B Volume 257, Issue 10, 1900140, October (2020).
A chiral 3D lattice was designed, made by 3D printing, and studied experimentally. The lattice exhibited squeeze-twist coupling and a Poisson's ratio near zero. Squeeze-twist coupling does not occur in classical elasticity which makes no provision for chirality. By contrast, chiral effects are allowed in Cosserat elasticity. An experimental squeeze-twist coupling strain ratio on the order of unity and a Poisson's ratio near zero are in reasonable agreement with prior finite element analysis of a lattice with similar structure, for which negative Poisson's ratio is anticipated for a sufficient number of cells.
journal doi link
preprint pdf
R. S. Lakes, Softening of Cosserat sensitivity in a foam: warp effects, International Journal of Mechanical Sciences, Volume 192, 106125, 15 February 2021.
Buckling gives rise to softening of the structural stiffness of columns; buckling of ribs gives rise to softening of the incremental elastic modulus of foams. Softening of Cosserat characteristic lengths occurs in pre-compressed foam material as determined from warp of cross sections of a square bar in torsion. Warp in the foam is reduced considerably in comparison with the predictions of classical elasticity. Pre-compression increases the warp in comparison with the warp observed without pre-compression. The effect is attributed to release of energy stored via pre-compression.
DOI link
preprint
D. R. Reasa and R. S. Lakes, Nonclassical Chiral Elasticity of the Gyroid Lattice, Phys. Rev. Lett. 125, 205502, 13 November (2020).
The gyroid lattice is a metamaterial which allows chirality that is tunable by geometry. Gyroid lattices were made in chiral and non-chiral form by 3D printing. The chiral lattices exhibited nonclassical elastic effects including coupling between compressive stress and torsional deformation. Gyroid lattices can approach upper bounds on elastic modulus. Effective modulus is increased by distributed moments but is, for gyroid cylinders of sufficiently small radius, softened by a surface layer of incomplete cells. Such size dependence is similar to that in foams is but unlike most lattices.
These may be called surface metamaterials.
journal link
preprint pdf
R. S. Lakes, "The corner element in classical elasticity and Cosserat elasticity", Journal of Mechanics of Materials and Structures (JOMMS), 16 (2) 225-235 (2021).
The corner element is considered in torsion of a square cross section bar. Understanding the corner element has a pedagogic role in mechanics of materials and elasticity and is also helpful in providing physical insight for generalized continuum theories such as Cosserat elasticity. Analysis of the corner element reveals the slope of the warp curve at the corner in a classical solid and approximates the slope of the warp curve in a Cosserat solid.
doi link
preprint pdf
R. S. Lakes, "Experimental tests of rotation sensitivity in Cosserat elasticity and in gravitation", Zeitschrift fuer Angewandte Mathematik und Physik (ZAMP) 72. 131 May (2021).
Experimental tests of rotation sensitivity in elastic materials and in empty space are surveyed. Pioneers in the theory for each field of study were aware of the other field. Sensitivity to rotation has been demonstrated experimentally in elastic solids but tests for rotation gradient sensitivity in gravity have found no such effects. Insight from comparison of experimental approaches may lead to new experimental protocols.
journal link,
doi link
preprint
T. DeValk and R. S. Lakes, "Poisson's ratio and modulus of the gyroid lattice", Physica Status Solidi B 258 (12) 2100081 (2021).
Gyroid surface lattices of different density exhibited Young's modulus consistent with stretch-dominated extremal behavior approaching the Hashin-Shtrikman upper bound. Gyroid lattices exhibited a Poisson's ratio of 0.34 independent of direction, independent of specimen diameter and independent of chirality. This behavior is in contrast with prior chiral lattices that exhibited pronounced size effects in Poisson's ratio, allowable for chiral elastic solids.
doi link
preprint pdf
R. S. Lakes, "Extreme Cosserat elastic hinged lattices with Sarrus links", Extreme Mechanics Letters 49, 101517 November (2021).
Hinged lattices are envisaged with Sarrus linkages in the ribs and with rigid nodes where the ribs intersect. Triangulated lattices with Sarrus hinged ribs only deform volumetrically and have a Poisson's ratio of -1. Lattices containing squares and hexagons can deform axially as well as volumetrically. All the lattices are compliant with respect to tension and compression and rigid with respect to bending. The lattices exhibit extreme Cosserat elasticity corresponding to rotational elasticity.
doi link
preprint pdf
R. S. Lakes, "Extremal hinged lattices do not obey the theory of elasticity", Zeitschrift fur angewandte Mathematik und Physik (ZAMP) 73:27 (2022).
Hinged lattices that attain extremal values of Poisson's ratio do not in general obey the theory of elasticity. Hinged structures that attain a Poisson's ratio of -1 are easy to stretch or deform volumetrically but they resist bending, in contrast to the predictions of elasticity theory. Their behavior corresponds to that of a Cosserat solid with divergent characteristic length. Hinged structures that attain a maximum Poisson's ratio are rigid with respect to hydrostatic tension, are easy to shear or to stretch but are unstable with respect to hydrostatic compression.
https://doi.org/10.1007/s00033-021-01664-x doi link
preprint pdf
Goyal, K. Rueger, Z., and Lakes, R. S., "Cosserat elasticity in the octet lattice" Journal of Mechanics of Materials and Structures (JoMMS) 16 (5) 645-654 (2021).
Size effects in effective modulus were of small magnitude, 30% in torsion and 10% in bending. The Cosserat characteristic lengths in torsion (1 mm) and in bending (0.5 mm) are considerably smaller than the cell size, 4.5 mm. The lattice is considered to be weakly Cosserat elastic.
doi link
preprint pdf
R. S. Lakes, "Cosserat shape effects in the bending of foams" Mechanics of Advanced Materials and Structures, accepted 2022. Volume 30, Issue 19 Pages 3997-4001 (2023).
In classical pure bending of a bar of square cross sections, two lateral surfaces undergo anticlastic curvature and the other two lateral surfaces undergo tilt. If the bar is made of a Cosserat solid, the tilted lateral surfaces deform in a sigmoid shape in addition to tilt. Parametric studies reveal the bulge depends on the bending characteristic length, the coupling number, and the ratio of two Cosserat rotation gradient constants. This sigmoid bulge deformation is observed in two foams and is found to be consistent with predictions using elastic constants obtained from size effect studies.
doi link https://doi.org/10.1080/15376494.2022.2086328
R. S. Lakes, B. Huey, and K. Goyal,"Extended Poisson's ratio range in chiral isotropic elastic materials", Physica Status Solidi B 259, (12), 2200336 (2022).
Poisson's ratio in chiral Cosserat elastic solids is considered. Chirality allows the Poisson's ratio to exceed classical bounds, even if the material is directionally isotropic and all elastic moduli are within thermodynamic limits based on strain energy density. Poisson's ratio in chiral rods depends on the chiral elastic constants as well as on the shear and bulk moduli, assumed positive. Poisson's ratio can be greater than 0.5 or smaller than -1 for slender chiral specimens.
doi link https://doi.org/10.1002/pssb.202200336
preprint pdf
T. DeValk, J. Hestetune, R. S. Lakes,"Nonclassical thermal twist of the chiral gyroid lattice", Physica Status Solidi B, 259, (12), 2200338 (2022).
The gyroid lattice was prepared in chiral and non-chiral forms. The chiral gyroid lattice was observed to exhibit temperature induced twist with direction of twist corresponding to the sense of chirality. This effect is a nonclassical effect that cannot occur in classical elasticity or classical thermo-elasticity but is allowable in Cosserat solids. Poisson's ratio of the gyroid is known to be about 0.3 with minimal dependence on size. In contrast to squeeze-twist coupling in which substantial size effects occur with slender specimens twisting much more than thicker ones, thermal-twist coupling exhibits opposite and less consistent size effects of much smaller magnitude.
doi link https://doi.org/10.1002/pssb.202200338
R. S. Lakes, "Experimental evaluation of micromorphic elastic constants in foams and lattices", Zeitschrift fur angewandte Mathematik und Physik (ZAMP), 74, Article number: 31 (2023).
Micromorphic (microstructure) elastic constants are considered within the context of experimental results for foams and rib lattices, and of subsets such as Cosserat elasticity, void elasticity and reduced micromorphic elasticity. Experimentally, longitudinal wave dispersion and cut off frequencies reveal several of the the micromorphic b coefficients. In static experiments, no size effects are evident in compression for the materials studied. The corresponding micromorphic a coefficients are not distinguishable from zero. By contrast, Cosserat effects are pronounced in these materials.
doi link https://doi.org/10.1007/s00033-022-01923-5
view link
R. S. Lakes, "Nonclassical Cosserat bending deformation of foams via holographic interferometry", Zeitschrift fur angewandte Mathematik und Physik (ZAMP) , 74, 153, 3 July (2023).
Nonclassical bending deformation in two foams was investigated using holographic interferometry. Sigmoid bulge deformation of the lateral surface of square cross section bars was observed. Cosserat elastic constants inferred are consistent with values obtained via size effect experiments for dense polyurethane foam. For open cell copper foam, both bulge measurements and size effects implied a large Cosserat characteristic length and a large coupling number. Limitations of the available fourth order bending analysis were encountered in this regime of strong effects.
doi link
SharedIt link view link: view
R. S. Lakes and B. Huey, "Poisson's ratio beyond the classically allowable range in chiral isotropic elastic materials: effect of kappa and experiment", Physica Status Solidi B Volume 261, Issue12, 2300411, December (2024).
Poisson's ratio in chiral isotropic elastic solids can be larger or smaller than the classical thermodynamic bounds. The effect of Cosserat coupling constant k is studied. Analysis shows that solids with weak coupling exhibit Poisson's ratio anomalies for larger specimen sizes than corresponding solids with strong coupling. Experiments on a quasi-isotropic composite with chiral inclusions show Poisson's ratio greater than 0.5.
First published: 14 November (2023). pdf available via agreement between publisher and the university.
doi link
Y. Wang, D. Stone, R. S. Lakes, "Cosserat sigmoid bulge effects in the bending of a lattice of tetrakaidecahedron cells", Z. Angew. Math. Phys. (ZAMP) 75:239, (2024).
doi link
sharing link
R. S. Lakes, "Nonclassical heat flow in passive chiral solids is third rank, not odd", ArXiV 2412.08309 (2024).
Chiral, directionally isotropic gyroid lattices are observed to exhibit nonclassical thermal effects incompatible with an asymmetric ("odd'') second rank conductivity tensor but consistent with a third rank tensor property that provides a curl term. The lattices are passive materials so no driving torques are needed to obtain transverse flow. A method for determination of the length scale associated with chirality is provided. The polymer gyroid lattice made by 3D printing is a metamaterial which allows chirality that is tunable by geometry.
link
This is a preprint of
R. S. Lakes, "Nonclassical heat flow in passive chiral solids is third rank, not odd", Z. Angew. Math. Phys. (ZAMP) 76: 81 (2025).
journal pdf
doi link
R. S. Lakes, "Materials that exceed classical thermodynamic bounds on properties", Reviews of Modern Physics, 97, 021002 14 May, (2025).
journal link
doi journal link
reprint pdf
Many aspects of freedom in materials are reviewed.
R. S. Lakes, "Cubic lattice rib shape: tuning of Poisson's ratio and Cosserat characteristic length", physica status solidi (b), accepted, Aug. (2025). First published: 20 August (2025). pdf available via agreement between publisher and the university.
doi link
Recent research involves experimental study of Cosserat elastic effects in open cell foams and of analysis of microstretch elasticity which contains Cosserat type freedom as well as sensitivity to dilatation gradient. Sensitivity to dilatation gradient cannot account for the effects observed in torsion, in which there is no dilatation. Cosserat effects are observed in negative Poisson's ratio foams.
Designed Cosserat lattices have been embodied physically via 3D printing and studied experimentally via optical methods. Tuning of Cosserat constants is possible. It is therefore possible to control asymmetric stress in materials. Such materials enable the designed reduction in stress concentration factors. Rib lattices are of particular interest in this context.
A subset of Micromorphic - microstructure elasticity has been studied as an alternate approach to generalized continuum theory by Professors Neff, Huetter, and Rizzi. The term "odd elasticity" has been used by others for a class of active materials. In some examples of this, distributed moments are incorporated. Properly they should be subsumed under active Cosserat elasticity.
As for other experiments, waves have been recently used by Merkel, Tournat, Gusev "Experimental evidence of rotational elastic waves in a granular phononic crystal". The system they used is an assembly of elastic spheres in contact. This is an ideal system, designed to exhibit only one Cosserat constant, kappa. Wave methods for Cosserat and other generalized continua are suitable for idealized elastic systems without dissipation as discussed in more detail in the linked page. For dissipative materials or systems, wave speed varies with frequency from both viscoelastic effects and dispersion from the microstructure. This complicates interpretation.
We have mostly done without the term metamaterial for designed Cosserat solids, though such terminology has recently become popular in referring to materials that attain interesting or extreme properties via structure rather than composition. Similarly we did not use the phrase materials by design or architectured materials or architected materials. Lattices comprised of ribs have been called truss metamaterials.
Top
Top









 Lakes, R. S. and Saha, S., "Cement line motion in bone," Science, 204,
501-503 (1979). Get pdf.
Lakes, R. S. and Saha, S., "Cement line motion in bone," Science, 204,
501-503 (1979). Get pdf.
 Continuum representations of micromechanical phenomena in structured materials are described, with emphasis on cellular solids. These phenomena are interpreted in light of Cosserat elasticity, a generalized continuum theory which admits degrees of freedom not present in classical elasticity. These are the rotation of points in the material, and a couple per unit area or couple stress. Experimental work in this area is reviewed, and other interpretation schemes are discussed. The applicability of Cosserat or micropolar elasticity to cellular solids and fibrous composite materials is considered as is the application of related generalized continuum theories. New experimental results are presented for foam materials with negative Poisson's ratios.
Continuum representations of micromechanical phenomena in structured materials are described, with emphasis on cellular solids. These phenomena are interpreted in light of Cosserat elasticity, a generalized continuum theory which admits degrees of freedom not present in classical elasticity. These are the rotation of points in the material, and a couple per unit area or couple stress. Experimental work in this area is reviewed, and other interpretation schemes are discussed. The applicability of Cosserat or micropolar elasticity to cellular solids and fibrous composite materials is considered as is the application of related generalized continuum theories. New experimental results are presented for foam materials with negative Poisson's ratios.

 This image shows computer generated fringe patterns associated with
This image shows computer generated fringe patterns associated with 



