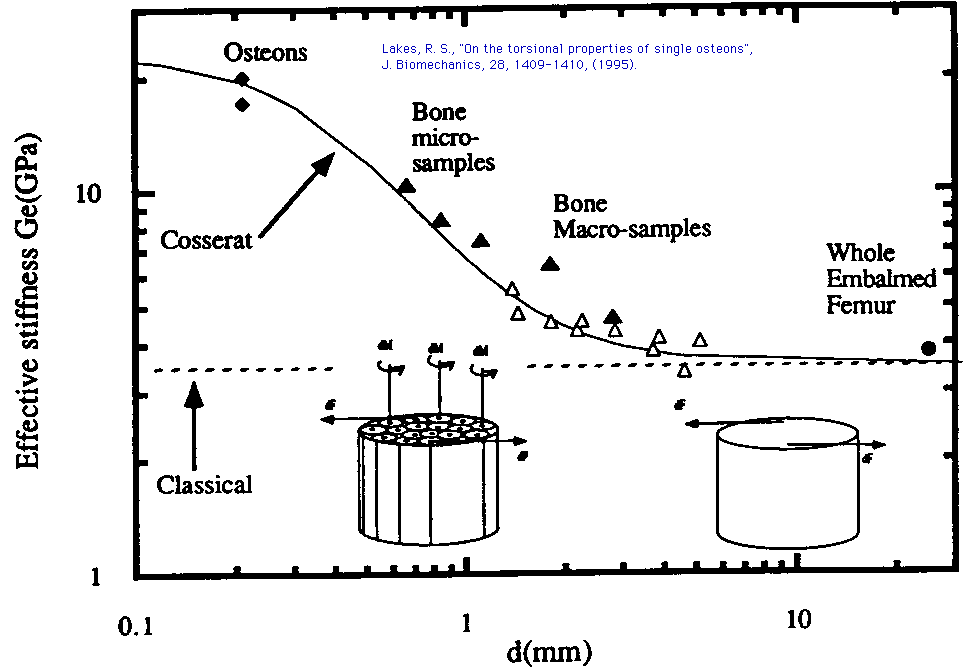
Fig. 1 Effective torsional stiffness vs diameter
-diamond- Osteons, fresh, wet, after Ascenzi, et. al., (1994).
Delta - Bone macro-samples, fresh, wet, after Yang and Lakes (1981).
Delta -Bone micro-samples, fresh, wet, after Lakes and Yang (1983).
* Whole embalmed femur, after Huiskes, et. al., (1981).
___ Solid curve, Cosserat elasticity, torsion, assuming technical elastic constants to be:
G = 3.5 GPa, l_t = 0.22 mm, l_b = 0.44 mm, Y (Psi )= 1.5, N = 0.62.
Apparent shear modulus seems to vary with diameter.
Inset drawings: right, classical elastic continuum with stress due to force increments dF;
left, bone as a Cosserat elastic continuum with both force increments dF
and torque increments dM upon osteons.
- - - - Dashed line: classical elasticity, torsion.
Apparent shear modulus is independent of diameter.

Ascenzi et. al. (1994) recently reported high shear moduli in bone mechanics tests upon wet single human femoral osteons of various fiber architectures. The shear moduli, 23 GPa for osteons with longitudinal fibers, and 17 GPa for osteons with lamellae of alternate orientation, were more than four times higher than moduli reported in the literature for macroscopic specimens of bone tissue. The authors discussed some artifactual processes which could have raised the moduli, as well as structural features of bone. We consider the authors' reported moduli to be correct as they stand. It is the purpose of this communication to elucidate the reasons, both in the structural view and in the continuum view, for the difference in moduli between osteons and bone.

Human bone is a natural composite with a very complex structure. The cement lines between osteons constitute a structural feature of prime importance in understanding the relationship between osteons and whole bone. Although the cement substance is not well characterized, we consider that there is substantial experimental and theoretical evidence that the cement lines as compliant interfaces account for most of the difference in stiffness between osteons and whole bone. Bone under prolonged torsional load (corresponding to very low frequency) exhibits localized slippage, sufficient to be observable as a microscopic displacement, at the cement lines in bovine plexiform bone (Lakes and Saha, 1979) and in human Haversian bone. Bone under load at high frequencies associated with ultrasonic tests is anisotropic, and the anisotropy is consistent with a composite theoretical model in which ground substance at the cement line was inferred to be about one quarter as stiff as the osteon (Katz, 1980). Since the ground substance is viscoelastic, it would be considerably less stiff at frequencies associated with physiological loading of bone.

Experiments on bone may also be interpreted within the continuum view in which the forces in the micro-structure are averaged, and concepts of stress and strain are used. In that vein, size effects in the rigidity of bone samples were reported by Frasca et. al. (1981) and by Yang and Lakes (1981, 1982) who also interpreted the results via a generalized continuum theory, Cosserat or micropolar elasticity, which allows a moment per unit area as well as the usual force per unit area. Slender specimens had a higher apparent stiffness than thick ones. The stiffening effect was noticeable even for specimens as thick as 5 to 6 mm. Such specimens would have a full complement of structural features such as Volkmann canals. Therefore the absence of such features in the single osteons of Ascenzi et. al. (1994) cannot substantially account for their higher stiffness. As for the magnitude of the ratio in stiffness of osteons to that of whole bone, a factor of 3.5 stiffening effect was observed by Roderic Lakes and J. F. C. Yang (1983) in microsamples as small as about 0.5 mm in diameter. The osteon stiffnesses reported by Ascenzi et. al. (1994) are in harmony with the torsional size effects observed by others, as shown in Fig. 1. The datum for an instrumented whole femur with 100 strain gage rosettes, after Huiskes et. al. (1981) is for embalmed bone, for which the longitudinal Young's modulus is about 12% greater than for fresh bone. The solid line represents a Cosserat continuum view which incorporates distributed moments (couple stress) as well as distributed forces (stress).

The experiments performed by Ascenzi et. al. (1994) are delicate ones, however we do not consider artifacts to be responsible for the high moduli, for the following reasons. As for the low aspect ratio of the stubby specimens, it might elevate the apparent modulus in tension or compression due to restraint of the osteon's Poisson effect. Such an effect is inoperative in torsion. Moreover, the end pieces, though they are much stiffer than the osteon in terms of elementary analysis of torsion are still made of bone; they offer some compliance in response to the concentrated torque presented by the osteon (see, e.g., Sneddon, (1951)). Therefore the effect of the end pieces is to lower the stiffness, not to raise it. As for end conditions restraining axial displacement, there are two such coupling processes between torsion and tension. One is a form of geometric nonlinearity; the effect is quadratic in strain and will not influence the evaluation of modulus at small strain. The other effect is linear in strain, but it depends on a chiral (noncentrosymmetric) anisotropy of the material (Lakes and Benedict, 1982), and understanding it involves a generalized continuum analysis of the material. Chiral effects may cause an osteon under axial constraint to appear stiffer. However osteons within whole bone are also under some axial restraint from the adjacent osteons and therefore would experience a similar stiffening.

Observations of osteon stiffness and understanding of its role in the generalized continuum representation of bone are important in that they bear upon the question of the toughness of bone. Bone is less vulnerable to the stress concentrating effects of drilled holes than is expected on the basis of classical elasticity (Brooks, et. al., 1970). The ability of bone to redistribute stress around such defects (prior to any remodeling) is associated with the alternate stress pathway of Cosserat elasticity (Park and Lakes, 1986) for which the physical mechanism is the array of local moments transmitted through the stiff osteons.

To conclude, the high torsional stiffness observed by Ascenzi et. al. (1994) in single osteons is consistent with prior experimental and theoretical work and is not to be regarded as a discrepancy. Moreover the osteon plays a role in conferring a measure of toughness upon bone.

References

Ascenzi, A., Baschieri, P., and Benvenuti, A., (1994) The torsional properties of selected single osteons, J. Biomechanics, 27, 875-884.

Brooks, D. B., Burstein, A. H., and Frankel, V. H., (1970) The biomechanics of torsional fractures: the stress concentration effect of a drill hole, J. Bone Jnt. Surg. 52A, 507-514.

Frasca, P., Harper, R., and Katz, J.L., (1981) Strain and frequency dependence of shear storage modulus for human single osteons and cortical bone microsamples - size and hydration effects, J. Biomechanics, 14, 679-690.

Huiskes, R., Janssen, J. D. and Slooff, T. J., (1981) A detailed comparison of experimental and theoretical stress analyses of a human femur, in Mechanical Properties of Bone Joint ASME-ASCE Applied Mechanics, Fluids Engineering and Bioengineering Conference, Boulder, Colorado, 22-24 June, 1981.

Katz, J. L., Anisotropy of Young's modulus of bone, (1980) Nature, 283, 106-107.

Lakes, R.S. and Benedict, R.L., (1982) Noncentrosymmetry in micropolar elasticity, International Journal of Engineering Science, 29 (10), 1161-1167.

Lakes, R.S. and Saha, S., (1979) Cement line motion in bone, Science, 204, 501-503.

Lakes, R.S. and Yang, J.F.C., (1983) Micropolar elasticity in bone: rotation modulus [[kappa]], Proceedings 18th Midwest Mechanics Conference, Iowa City, Developments in Mechanics, Vol. 12, p. 239-242.

Park, H.C. and Lakes, R.S., (1986) Cosserat micromechanics of human bone: strain redistribution by a hydration-sensitive constituent, J. Biomechanics, 19 385-397.

Sneddon, I. N., (1951) Fourier Transforms, McGraw Hill, NY; p. 501-504.

Yang, J.F.C., and Lakes, R.S., (1981) Transient study of couple stress in compact bone: torsion, Journal of Biomechanical Engineering, 103, 275-279.

Yang, J.F.C., and Lakes, R.S., (1982) Experimental study of micropolar and couple stress elasticity in bone in bending, Journal of Biomechanics, 15, 91-98.