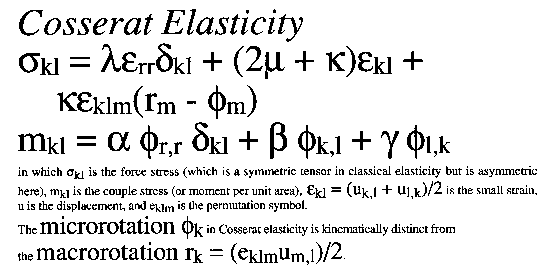Waves in Cosserat elasticity / micropolar elasticity
Cosserat elasticity main page
Experiment , dense foams
Bone and osteons
Chiral composites
The Cosserat theory of elasticity, also known as micropolar elasticity, the micropolar theory of elasticity, or micropolar continuum mechanics, incorporates a local rotation of points as well as the translation assumed in classical elasticity; and a couple stress (a torque per unit area) as well as the force stress (force per unit area). The force stress is referred to simply as 'stress' in classical elasticity in which there is no other kind of stress.
In the isotropic Cosserat solid or micropolar continuum, there are six elastic constants, in contrast to the classical elastic solid in which there are two independent elastic constants. The micropolar theory also incorporates a micro-inertia that is pertinent to dynamic deformation at sufficienly high frequency.
Waves
In a Cosserat solid [1] with the micro-inertia incorporated in the micropolar formulation, dispersion of shear waves [2] is expected to occur. In particular, the wave speed of plane dilatational waves in an unbounded Cosserat elastic medium is independent of frequency as in the classical case, that is, no dispersion. The speed of shear waves depends on frequency in a Cosserat solid. A new kind of wave associated with the micro- rotation is predicted to occur in Cosserat solids. Wave dispersion also occurs in the Mindlin microstructure theory [3] and in nonlocal solids [4]. A theory similar to Mindlin microstructure theory was called micromorphic by Eringen. In such theories the points in a continuum may translate as in classical elasticity, rotate as in Cosserat elasticity, and deform as well. The isotropic Cosserat solid has 6 independent elastic constants. The isotropic micromorphic / microstructure solid has 18 independent elastic constants.
If wave methods are to be used in experiments [5], a difficulty is that wave dispersion also arises from viscoelasticity of materials. Wave methods are therefore most suitable if the wave attenuation due to viscoelasticity is small enough to be neglected. In viscoelastic materials, all material coefficients, including the Cosserat ones, can depend on time or frequency. One must therefore decouple the frequency dependence associated with the material coefficients from the wave dispersion associated with the generalized continuum, e. g. Cosserat, model. This cannot be done in wave methods, since the wavelength which governs the strain gradient cannot be decoupled from the frequency. Moreover, dispersion may be so strong that no transmitted waves are discerned.
Experiments
A wave method was used by Gauthier [6] to examine the particulate composite consisting of aluminum spheres embedded in an epoxy matrix. This material had appeared classical in the quasi-static size effect studies of Gauthier and Jahsman [7]. The micro-inertial characteristics were determined, and it was found that the coupling number N2 = 0.0039. This is so small that the static behavior would appear classical regardless of the characteristic length, which appears to be zero. Indeed, composite materials containing elliptic or spherical inclusions are predicted to have a Cosserat / micropolar characteristic length of zero (Hlavacek, [8]; Berglund, [9]).
Waves have been recently used by Merkel, Tournat, Gusev [10]. The system here is a constrained assembly of elastic spheres in contact. This is an ideal system, designed to exhibit only one Cosserat constant, expressed in the notation of Nowacki [11]. The lattice of steel spheres is expected to behave elastically with minimal viscoelastic dissipation, hence amenable to the wave method, provided frictional dissipation does not occur. As with beaded composites [6][8][9], the characteristic length, which gives rise to size effects and toughness, is zero by analysis.
As for real materials, the difficulty with using waves to explore Cosserat effects is that wave speed depends on frequency both from geometrical dispersion (such as Cosserat or micropolar type) and from viscoelastic dispersion. It is not so easy to separate these effects in real dissipative materials. We have done ultrasound studies in bone, known as a Cosserat solid from prior experiments, but viscoelastic effects and other effects tend to dominate the behavior. Slow waves were, however, observed, and these were attributed to fluid - solid interaction in wet bone. See selected articles, slow waves. Cosserat elastic constants have been calculated based on reported dispersion of acoustic waves in diamond crystals [12]. As might be expected, the characteristic length in on the order of the spacing of atoms in the crystal lattice.
We have done some experiments on dispersion of longitudinal waves; these experiments indicate micromorphic / microstructure elastic freedom.
References
1. E. and F. Cosserat, Theorie des Corps Deformables. A. Hermann et Fils, Paris, 1909.
2. A. C. Eringen, Theory of micropolar elasticity. In Fracture (Edited by H. Liebowitz) Vol. 2, pp. 621- 729. Academic Press, New York, 1968.
3. Mindlin, R. D., Micro-structure in linear elasticity, Arch. Rational Mech. Analy, 16, 51-78, 1964.
4. Eringen, A. C., Linear theory of nonlocal elasticity and dispersion of plane waves, Int. J. Engng Sci, 10, 425-435, 1972.
5. Lakes, R. S., Experimental methods for study of Cosserat elastic solids and other generalized continua, in Continuum models for materials with micro-structure, ed. H. Muhlhaus, J. Wiley, N. Y. Ch. 1, p. 1-22, 1995. Review article pdf
6. Gauthier, R. D., Experimental investigations of micropolar media, In Mechanics of micropolar media, ed. O. Brulin, R. K. T. Hsieh, World Scientific, Singapore, 1982.
7. Gauthier, R. D. and W. E. Jahsman. A quest for micropolar elastic constants. J. Applied Mechanics, 42, 369-374, 1975.
8. Hlavacek, M., On the effective moduli of elastic composite materials, Int. J. Solids and Structures, 12, 655-670, 1976.
9. Berglund, K., Structural models of micropolar media, in Mechanics of Micropolar Media, edited by O. Brulin and R. K. T. Hsieh, World Scientific, Singapore, 1982.
10. Merkel, Tournat, Gusev Experimental evidence of rotational elastic waves in a granular phononic crystal, Phys. Rev. Lett. 2011.
11. Nowacki, W., Theory of micropolar elasticity, Poznan, 1970.
12. M. Nagawa, K. Arakawa, M. Yamada, Diamond Crystals as Cosserat Continua, phys. stat. sol. (a) 57, 713-718 (1980).
Cosserat equations, using the equations of Eringen for micropolar elasticity are as follows. Other authors use different symbols.
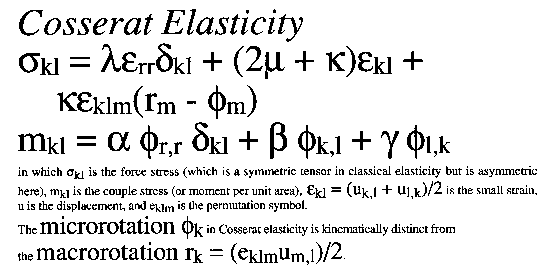
Cosserat equations. Click on image for larger image.
Top