Abstract
Consequences of noncentrosymmetry in a micropolar or Cosserat elastic solid are considered.
A solid which is isotropic with respect to coordinate rotations but not with respect to inversions is called noncentrosymmetric, acentric, hemitropic, or chiral. Chirality (hemitropy) has no effect upon the classical elastic modulus tensor. In Cosserat elasticity, chirality has an effect. A chiral Cosserat solid has three new elastic constants in addition to the six considered in the fully isotropic micropolar solid.
A chiral or hemitropic micropolar cylindrical rod is predicted to undergo torsional deformation when subjected to tensile load, so a chiral composite will twist when stretched. Thus chiral solids have different mechanical behavior from solids with a center of symmetry, as allowed by the more general Cosserat elastic theory. These concepts lay the groundwork for chiral metamaterials or chiral architectured materials or chiral architected materials; we did not use such terminology. Use of 3D printing facilitates making such materials.
1. INTRODUCTION
Generalized continuum theories for mechanical behavior developed over the last century admit degrees of freedom not considered in the classical theory of elasticity. Common to such theories as those of the Cosserats [l], the indeterminate couple stress theory of Mindlin and Tiersten [2] and the micropolar theory of Eringen [3] is the assumption of couple stress and the associated asymmetry of the force stress tensor. Generalized continuum theories are thought to have applications in the modeling of materials with microstructure, such as granular or fibrous materials, or materials with a lattice structure. Micropolar theory has in recent years stimulated considerable interest, and analytical solutions to many problems in micropolar elasticity are available. Of particular interest to the experimentalist are the predictions of size effects in the apparent stiffness of a cylindrical member in torsion [4] and in bending [5]. In most published solutions, material isotropy is assumed. Some materials, however, are not invariant to coordinate inversions and this type of anisotropy can be expected to result in qualitatively different behavior in comparison with isotropic solids. Some aspects of initial stress in noncentrosymmetric Cosserat continua have been examined [6] but geometries addressable experimentally were not considered. Structural noncentrosymmetry is characteristic of bone, as well as synthetic composites containing twisted fibers. In this paper the behavior of a noncentrosymmetric micropolar elastic solid is examined.
2. NONCENTROSYMMETRIC MICROPOLAR THEORY
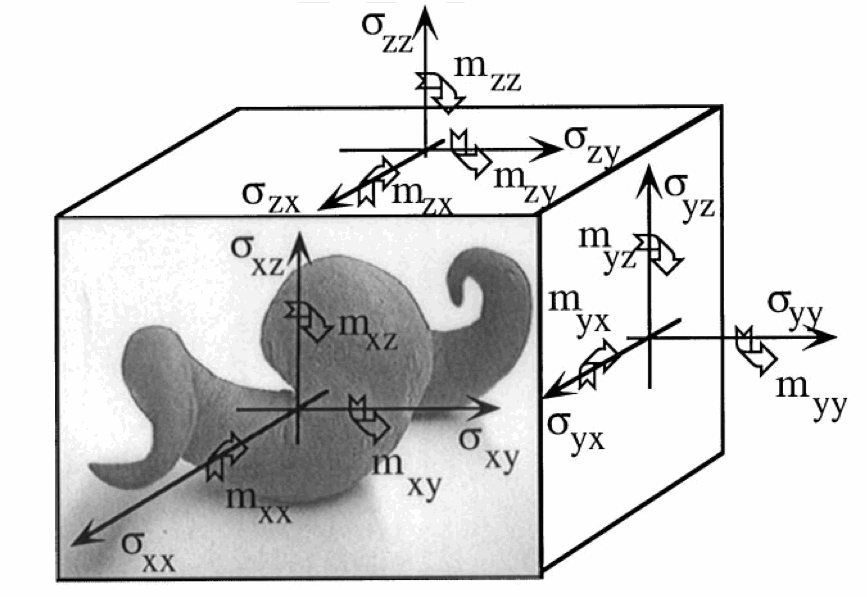
In classical elasticity, inversion symmetry has no effect on the elastic modulus tensor as shown in the following.
Greek sigma is shown as s; Greek delta may look like a bold face Latin d.

These are the constitutive equations for a micropolar solid which is isotropic with respect to coordinate rotations but not with respect to inversions.
Elastic constants C1, C2 and C3 are associated with noncentrosymmetry; if these vanish, the equations of isotropic micropolar elasticity are recovered. Consider micropolar elastic constants; if these also vanish, eqns (2.8) and (2.9) reduce to the constitutive equations of classical isotropic, linear elasticity theory, in which we have the Lame constants. Boundary conditions do not depend on assumed material symmetry. One may prescribe the displacements or the surface traction and the microrotations, or the surface couples on the surface which has exterior normal. If tractions are specified, the boundary conditions are given. [3]. The laws of motion also are independent of material symmetry and are given by [3].
3. RESTRICTIONS ON MICROPOLAR ELASTIC MODULI
In order that our noncentrosymmetric micropolar solid be stable, it is necessary that the internal energy be nonnegative. From this requirement, one may obtain restrictions on the micropolar elastic moduli. Consider the internal energy. Using the definitions, we may rewrite the energy, as seen in the original article in the library. Observe that the quantities can be varied independently of one another. If the first bracketed term in eqn (3.2) is the only one present, the requirement that this term be nonnegative yields Eq. (3.3) as in classical elasticity; a quantity is identified with the Lame shear modulus. The energies represented by the second, third and fourth terms must each be nonnegative, so for psi to be nonnegative it is necessary that Eq. (3.4) be true, a result obtained by Eringen for the fully isotropic micropolar solid. The product terms containing both the strain e and the micro-rotation phi cannot exist independently of the first-fourth terms, therefore, the above approach cannot be used to restrict the C coefficients; they can be positive or negative. However, for the total energy term to be nonnegative, it is necessary that a negative product term not be greater in magnitude than the sum of the corresponding positive terms containing e and A individually.
The C coefficients associated with noncentrosymmetry are bounded by products of combinations of classical elastic and micropolar coefficients. The quantities K are analogous to the coupling coefficients developed in the linear theory of piezoelectricity, and can be obtained in a similar fashion. This correspondence is anticipated on the basis of the formal similarity between the constitutive equations of linear piezoelectricity and those of noncentrosymmetric micropolar elasticity, eqns (2.3) and (2.4).
4. SIMPLE TENSION
Consider a cylindrical rod of radius R, of a noncentrosymmetric micropolar elastic solid. Let the rod be stretched by an axial force F, and let it be free of rotational constraint, and let the lateral surface be free of force traction and couples. Such a situation is relatively easy to realize experimentally, and serves to illustrate the effects of the C coefficients. To solve this tension problem, it is useful to express the constitutive equations, equilibrium equations and strain-displacement relations in cylindrical polar coordinates. The constitutive equations may be written as in the original article. The equilibrium equations are given. The micropolar strains in terms of the displacements and microrotations are given. In the case of simple tension of a long cylindrical rod of radius R, the following field of displacement and microrotation gives rise to a solution. Here I is the modified Bessel function of first order.

We may identify e with the axial strain and b0 with a twist angle per unit length of rod, arising from the coupling produced by the C coefficients. We observe that the Poisson-like contraction is not associated with a uniform radial strain as is the case in classical elasticity or in centrosymmetric micropolar elasticity [4].
The quantities are obtained by solving simultaneously the boundary condition equations for zero force traction and zero couple on the lateral surface of the rod, and zero net torque at the ends. The values are given in the manuscript.
In the above, the following quantities have been defined in terms of the micropolar elastic constants.
Additional quantities are defined, in which we have modified Bessel functions of order zero, one and two, respectively.
It is instructive to examine several special cases. If several parameters vanish, the twist angle per unit length is given in the original manuscript.
The twist angle is proportional to the axial strain e and to the coupling factor K0, and it tends to increase as the cylinder radius decreases. The twist angle can be positive or negative, depending on the sign of K0. A second special case is obtained by constraining the micro-rotation to be equal to the macrorotation. This constraint yields a solution to the tension problem in noncentrosymmetric indeterminate couple stress theory. The constraint is achieved by allowing p to become infinitely large. The twist angle per unit length becomes as given in the original manuscript.
In both special cases the twist angle is proportional to the coupling factor K0 and the axial strain e. For a thick rod of radius R much greater than the Cosserat characteristic length, the twist angle increases as the inverse square of the radius. For a sufficiently small radius compared to the characteristic length (an unphysical situation), the twist angle per unit axial strain approaches a constant value.
5. PHYSICAL INTERPRETATION
The quantities l0 - l4 have dimensions of length and may be referred to as characteristic lengths. l0 is the characteristic length defined in connection with the problem of torsion in centrosymmetric micropolar theory by Gauthier and Jahsman [4]. In generalized continuum models of structured materials, the characteristic lengths are generally found to be related to the size of structural elements. The quantities K1 - K5 are dimensionless. K0 and K1 are measures of the strength of the noncentrosymmetric coupling and are analogous to the coupling coefficients of piezoelectricity theory. K4 is equivalent to the classical Poisson ratio, since mu + kappa /2 is the observed shear modulus. K2 and K3 are similar in nature to K4, as seen by comparing the role of lambda with that of C1 and alpha in eqns (2.8) and (2.9). K5 represents the strength of coupling between the macrostrain field and the microrotation field.
Micropolar elasticity and related continuum theories are thought to apply to granular, fibrous, or composite materials. The noncentrosymmetric theory is intended for solids containing twisted or spiraling fibers, in which one direction of twist or spiral predominates. If the fibers are distributed randomly in all directions, tensile specimens taken in any orientation will appear to have the same Young's modulus, giving the impression of isotropy. Materials may exhibit handedness on the atomic scale, as in quartz and in biological molecules. Materials may also exhibit handedness on a larger scale, as in composites with helical or screw shaped inclusions. Such materials can exhibit odd rank tensor properties such as piezoelectric response. They may exhibit torsional deformation when stretched. A material such as aluminum crystallizes in a face-centered cubic lattice which has a center of symmetry, hence no handedness.
6. EXPERIMENTAL
Few experiments of any kind have been performed (prior to this manuscript date in 1982) to explore micropolar effects in real materials. Efforts to find effects describable by indeterminate couple stress theory in metals and by micropolar theory in a composite have been unsuccessful. Recently one of the authors (R.L.) has found evidence of couple stress effects in human compact bone [7,8]. There is some indication that micropolar theory is to be preferred over indeterminate couple stress theory in describing these effects. Regarding effects due to noncentrosymmetry, positive but very preliminary experimental results have been found [9].
Ropes and cables containing fibers which spiral are structurally noncentrosymmetric. It is well known that they untwist when subjected to tensile force with no constraint on rotation, as predicted in Section 4. Use of a continuum model for ropes is. however, questionable.
Future experiments seeking to demonstrate micropolar behavior could be performed using the tension mode described in Section 4. This is an attractive modality since great sensitivity is possible. It should be possible to detect acentric micropolar effects even if the structural asymmetry is on the atomic or molecular scale. For example, a fiber 0.07 mm dia. and 200 mm long is typical of boron-epoxy fibers used in composites. If such a fiber were subjected to an axial strain, the untwisting due to noncentrosymmetry could be detected by a reflected laser beam.
Experiments based on the results in Section 4 are capable of detecting micropolar behavior, but calculation of the nine elastic constants will be less than straightforward. A similar complexity in the combination of elastic constants is found in earlier work on centrosymmetric micropolar theory [4,5]. From the experimentalist's point of view, it appears that further attention to the solution of micropolar boundary value problems is warranted.
7. DISCUSSION
Several consequences of noncentrosymmetry in micropolar elasticity have been considered. Torsion deformation in response to tensile load, and size effects in Poisson's ratio are predicted. Very sensitive experiments based on the predicted behavior are possible. Macroscopic noncentrosymmetric micropolar effects may occur in chiral composite materials with twisted or spiraling fibers.

