Advances in negative Poisson's ratio materials
adapted from Advanced Materials , 5, 293-296, (1993). Diagrams at bottom.
get reprint pdf
Preface
Negative Poisson's ratio material expands laterally when stretched, in contrast to ordinary materials. Negative Poisson's ratio foam was first developed by Rod Lakes. Later writers have called such materials anti-rubber, auxetic, or dilatational.
Get preprint pdf of this article. get reprint pdf. A more recent (2017) review is available. Lakes, R. S., "Negative-Poisson's-Ratio Materials: Auxetic Solids", Annual Review of Materials Research, 47: 63-81 July (2017). Annual Reviews link.
1. Introduction
Poisson's ratio of a solid is defined as the lateral contraction strain divided by the longitudinal extension strain in a simple tension experiment. In almost all materials the Poisson's ratio, usually denoted by [[nu]], is positive. For isotropic materials (those in which the properties are independent of direction), energy arguments in the theory of elasticity [1] may be used to show that
Poisson's ratio [[nu]] is between -1 and 0.5.
The relationship between shear modulus G, bulk modulus K, and Poisson's ratio [[nu]] for isotropic materials is
G = (3K (1 - 2[[nu]]) / 2 (1 + [[nu]])) .
Most common materials have a Poisson's ratio close to 1/3, however rubbery materials have values approaching 1/2; they readily undergo shear deformations but resist volumetric (bulk) deformation, so G is much less than K above. Although textbooks can still be found which categorically state that Poisson's ratios less than zero are unknown, there are in fact a number of examples of negative Poisson's ratio solids. Such solids become fatter in cross section when stretched. A solid with [[nu]] close to -1 would be the opposite of rubber: difficult to shear but easy to deform volumetrically: G much greater than K. Therefore it may be called anti-rubber. In several cases negative Poisson's ratio was observed in an existing material; in several it was deliberately introduced by design. This article deals with materials with negative Poisson's ratios, how they can be created with specified properties, implications of these unusual physical properties, and recent advances.
2. Negative Poisson's ratio cellular solids
We consider first cellular solids with a negative Poisson's ratio, since the physical causes of the behavior of these solids are most readily appreciated. Two dimensional honeycombs with inverted cells (Fig. 1; compare with conventional honeycomb in Fig. 2) were reported with negative Poisson's ratios in the honeycomb plane [2-5], and these honeycombs have been recently analyzed [6,7]. Honeycombs are sufficiently simple that the Poisson effect can be easily visualized. Macroscopic structures in two or three dimensions consisting of rods, springs, and sliders, were devised to give a negative Poisson's ratio [5]; these structures have an inverted characteristic similar to the honeycombs. Structures of the above type require some form of individual
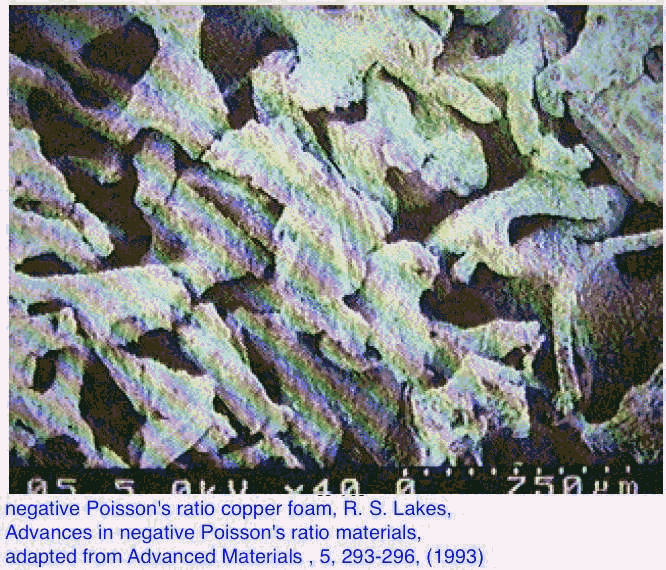
assembly. Foam materials with a negative Poisson's ratio as small as -0.7 were developed [8] in which an inverted or re-entrant cell structure was achieved by isotropic permanent volumetric compression of a conventional foam, resulting in microbuckling of the cell ribs. Polymer foams which exhibit a softening point [8,9], ductile metallic foams [8,9], and thermosetting polymer foams [9] can be prepared with a negative Poisson's ratio; [[nu]] ~ -0.8 can be attained in copper foam (Fig. 3). The negative Poisson's ratio occurs over a range of strain [10,11] and that range is larger in the polymer than in the metal foams. In the above structures and materials, the negative Poisson's ratio arises from the unfolding of the re-entrant cells, and isotropy can be achieved along with the negative Poisson's ratio. Anisotropic microcellular foams were recently reported to exhibit an unintentional negative Poisson's ratio in some directions [12,13]. Since these are anisotropic materials, the bounds on Poisson's ratio are wider ([[nu]] between -infinity and infinity) than in the isotropic case; indeed Poisson's ratios smaller than -1 have been reported. The physical mechanism appears to be associated with tilting of particulates linked by microfilaments.
Microcracks in a material can be viewed as flattened pores with minimal volume. Several types of rocks with microcracks have been reported to exhibit a negative Poisson's ratio [14,15] of about -0.1; the effect is abolished under water saturation or hydrostatic pressure.
As for recent advances, microporous polyethylene has been synthesized which exhibits a negative Poisson's ratio in a preferred direction [16]; some implications were discussed in a recent review [17]. The material was created by compacting powdered polymer, sintering, and extrusion. The final microstructure consisted of particles connected by fibrils. The polyethylene was mechanically anisotropic following the extrusion, with Poisson's ratios as small as -1.24 for compression in the radial direction, and zero for compression in the axial direction.
3. Negative Poisson's ratio composites
Several cases of negative Poisson's ratios have been discovered in the analysis of anisotropic fibrous composites. In some laminates composed of fibrous layers it is theoretically possible to achieve a negative Poisson's ratio as small as -0.21 in the direction perpendicular to the layers by control of the stacking sequence [18]. In other laminates, one can achieve a negative Poisson's ratio in some directions in the plane of the laminate, again by control of the stacking sequence [19,20]. In these composites there is a high degree of anisotropy and the negative Poisson's ratio only occurs in some directions; in some cases only over a narrow range of orientation angle between the applied load and the fibers.
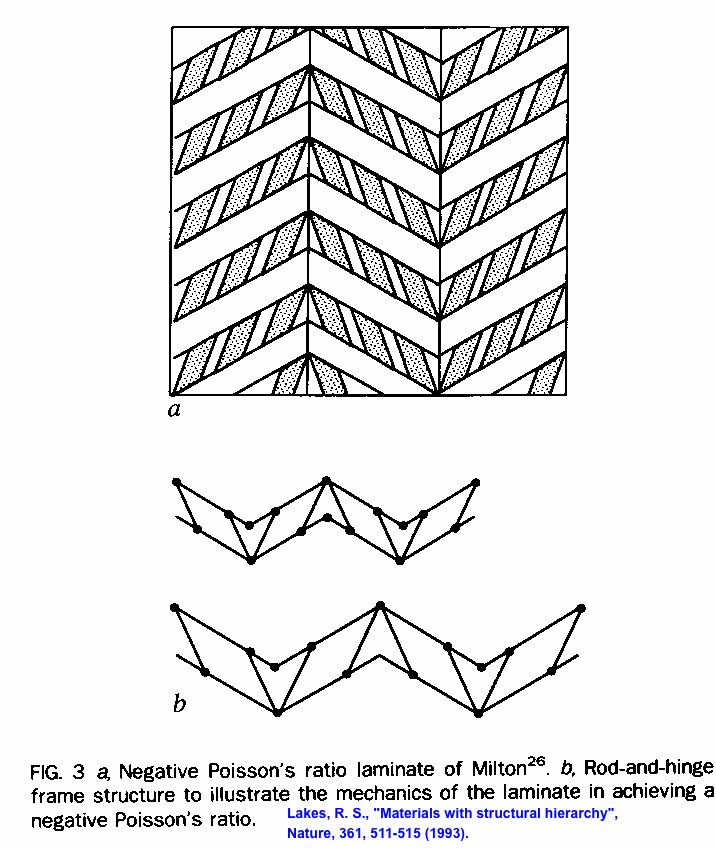
In a recent advance, laminate structures have been presented which give rise to intentional negative Poisson's ratios combined with mechanical isotropy in two dimensions (Fig. 4) or in three dimensions [21]. These laminates have structure on several levels of scale; they are hierarchical. By appropriate choice of constituent properties one can achieve Poisson's ratios approaching the lower limit of -1. The laminate Poisson's ratio is close to the rigorous lower bound which is independent of the microstructure, therefore it will not be possible to find microstructures with much lower Poisson's ratio for given constituent stiffnesses.
4. Crystalline and amorphous negative Poisson's ratio materials
A large compilation of elastic constants for single crystals and calculated elastic constants for polycrystalline aggregates made from them has been prepared [22]. Most polycrystalline materials have Poisson's ratio in the vicinity of 1/3, although beryllium has a value of about 0.1 and ammonium chloride is said to assume a negative value over a narrow temperature range.
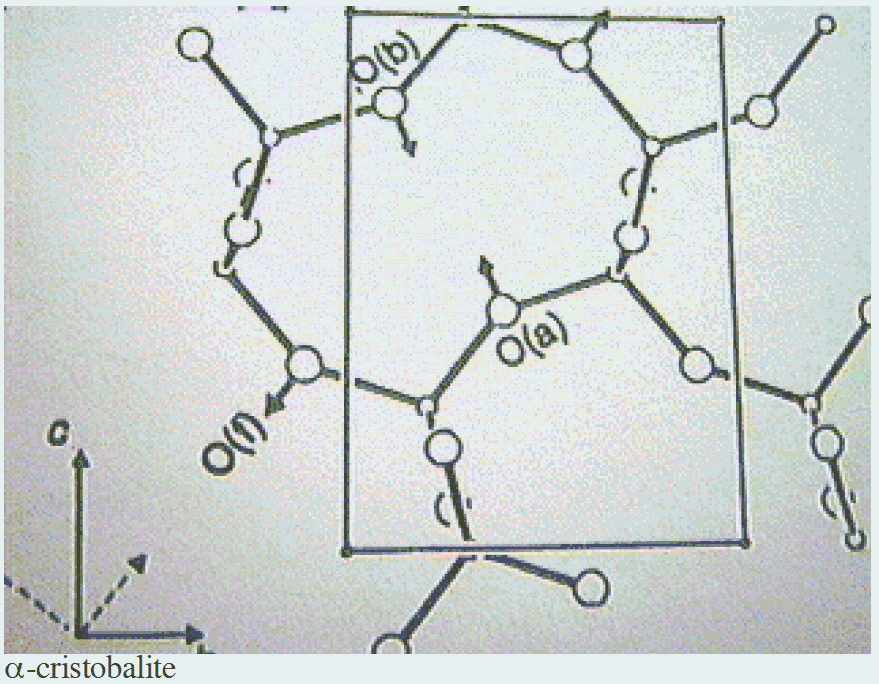
An early report suggested that a negative Poisson's ratio ([[nu]] ~ -1/7) occurred in single crystal iron pyrites [23], however recent study contradicts that claim [24]. A negative Poisson's ratio as small as -0.4 in certain directions was calculated [25] from published data on single crystal cadmium. Arsenic, antimony, and bismuth are highly anisotropic in single crystal form, and arsenic is the most anisotropic of these [26], with a factor of 11.3 variation in Young's modulus with direction. Poisson's ratios calculated for these materials are negative in some directions. Arsenic is so anisotropic that Poisson's ratio can exceed 0.5 or be less than -1 depending on direction of stress. The crystals contain a layered structure with weak binding between pairs of layers. A crystalline form of silica (SiO2), [[alpha]]-cristobalite, exhibits Poisson's ratios of +0.08 to -0.5, depending on direction [27]. Moreover, the Voigt and Reuss bounds for the Poisson's ratio of polycrystalline [[alpha]]-cristobalite are -0.13 and -0.19, with an averaged value of -0.16. Compared with the quartz form of silica, [[alpha]]-cristobalite is described as being more compliant, and with a more open crystal structure (Fig. 5). Pyrolytic graphite [28] intended for thermal protection in aerospace uses was found to have a negative Poisson's ratio of -0.21 in one crystallographic direction.
Certain ferromagnetic films [29] exhibited a negative Poisson's ratio which decayed with time. Several rare earth alloys (Sm1-xYxS) exhibit negative Poisson's ratios in the vicinity of a valence transition, for certain concentration values [30]; experiments disclose values as small as -0.7. The effect is attributed to a longitudinal mode softening which causes the bulk modulus to tend to zero at a critical concentration. The root cause of this is thought to be a high compliance of the rare earth ion [31]. A different type of phase transition was reported in certain types of polymer gels in which Poisson's ratio becomes negative (to about -0.4) over a narrow temperature range [32].
Common aspects of the unusual crystalline materials include a high degree of anisotropy. In the case of [[alpha]]-cristobalite, an isotropic solid made of randomly oriented crystals would exhibit a negative Poisson's ratio.
5. Causal mechanisms
Negative Poisson's ratios are unusual and counterintuitive; it is natural to inquire what is the cause of such an unusual physical property. Causes must be sought in the microstructure, since the continuum theories of elasticity do not specify particular values of Poisson's ratio. If the solid is made of atoms interacting by central forces, and the atoms move in an affine manner (locally equivalent to a strain combined with a rotation) under deformation, then Poisson's ratio is 1/4 [33,34]; the result is originally due to S. D. Poisson. Clearly, these assumptions are not satisfied even for most ordinary materials, since Poisson's ratio is typically close to 1/3. As for negative Poisson's ratio foams, it had been suggested that the effect is due to bending of the cell ribs [35], which can be subsumed into a Cosserat continuum model which has more freedom than classical elasticity; a possible role of Cosserat elasticity has also been considered in a study of mechanical models for materials with a negative Poisson's ratio [36]. Although foams indeed can have this extra freedom [37], it is not a likely cause of the negative Poisson's ratio [38]. Negative Poisson's ratios cannot be achieved via the bending or twisting rigidity of the cell ribs alone [39]. Non-affine (locally inhomogeneous) deformation by itself can give rise to the negative Poisson's ratio effects [40]. Other possible causes are pre-strain in the lattice structure [39] or a chiral structure [39,40]. Several illustrative models involving truss elements with sliders, and hypothetical granular structures, have been presented [41, 42].
In the re-entrant foams and honeycombs, inhomogeneous, non-affine deformation is manifested as an unfolding of the cells as the entire structure is extended; such deformation has been experimentally observed in foams [43]. The effect of microcracks would also appear to have a non-affine character. Simple analysis shows that cracks reduce the Poisson's ratio, negative values are not accounted for [44]. The structure of some of the crystalline materials, notably [[alpha]]-cristobalite and arsenic, suggests that non-affine deformation occurs.
6. Future possibilities
6.1 Applications
Applications of negative Poisson's ratio materials may be envisaged based on the Poisson's ratio itself, or based upon another unusual physical property which results from the underlying structural causal mechanism. The Poisson's ratio of a material influences the transmission and reflection of stress waves [45,46], the decay of stress with distance according to Saint Venant's principle [47], and the distribution of stress around holes and cracks [8,48]. The lateral deformation of negative Poisson's ratio materials may be of use in new kinds of fasteners [49]. Such materials may also find use in sandwich panels. When a plate or bar is bent, it assumes a saddle shape if Poisson's ratio is positive, and a convex shape if Poisson's ratio is negative [8,48,50-52]. The convex shapes are more appropriate than saddle shapes for sandwich panels for aircraft or automobiles. Stress distribution in a flexible pad such as a wrestling mat is more favorable to reducing impact forces upon both small objects such as an elbow and large objects such as a leg or back, if Poisson's ratio is as small as possible [48]. As for other physical properties, resilience [8,9,11] and sound absorbing capacity [53] are characteristic of the re-entrant foams. Hopefully some of these suggested applications will come to fruition.
6.2 New materials
In some applications it is essential to have a material which is stiff and strong. This is difficult to achieve in a foam. It is natural to ask, following consideration of causal mechanisms, if there must be empty space in the structure in order to achieve a negative Poisson's ratio. Single
crystals may contain relatively close packed atoms, but they are highly anisotropic. In any case the crystalline materials with a negative Poisson's
ratio described above are not well suited to structural applications. The hierarchical composites of Milton [21] offer the intriguing possibility of stiff materials with a negative Poisson's ratio via concepts of structural hierarchy. However the stiffness of one the two constituents must be at least 25 times greater than that of the other constituent to obtain a Poisson's ratio less than zero. A Poisson's ratio approaching -1 requires constituents which differ even more in stiffnesses, so that one phase is very soft, tending to 'empty space' in its properties. Another intriguing possibility is that of creating stiffer negative Poisson's ratio materials by design on the molecular scale [54]. It might be possible to make use of the existing free volume which exists in polymeric materials to achieve this goal [54]. Inspiration for future designs of new materials could be drawn from some of the material microstructures described in this article.
References
[1] Y. C. Fung, "Foundation of Solid Mechanics" Prentice-Hall, Englewood, NJ, 1968 p.353.
[2] G. S. Schajer and C. I. Robertson, "Mechanical behaviour of cellular structures", project report, Pembroke college, Cambridge University, 1974.
[3] L. J. Gibson, M. F. Ashby, G. S. Schajer, and C. I. Robertson, "The mechanics of two dimensional cellular solids", Proc. Royal Society London, 1982, A382, 25-42.
[4] A.G. Kolpakov, "On the determination of the averaged moduli of elastic gridworks", Prikl. Mat. Mekh 1985, 59, 969-977.
[5] R. F. Almgren, "An isotropic three dimensional structure with Poisson's ratio = -1", J. Elasticity, 1985, 15, 427-430.
[6] T. L. Warren, "Negative Poisson's ratio in a transversely isotropic foam structure", J. Appl. Physics, 1990, 67, 7591-7594.
[7] L.J. Gibson and M. Ashby, Mechanics of cellular solids, Pergamon, 1988.
[8] R. S. Lakes, "Foam structures with a negative Poisson's ratio", Science , 1987, 235 1038-1040.
[9] E.A. Friis, R.S. Lakes, and J.B. Park, "Negative Poisson's ratio polymeric and metallic materials", Journal of Materials Science, 1988, 23 4406-4414.
[10] Choi, J. B. and Lakes, R. S., "Nonlinear properties of metallic cellular materials with a negative Poisson's ratio", J. Materials Science, 1992, 27, 5373-5381.
[11] Choi, J. B. and Lakes, R. S., "Nonlinear properties of polymer cellular materials with a negative Poisson's ratio", J. Materials Science, 1992, 27, 4678-4684.
[12] B.D. Caddock, and K.E. Evans, "Microporous materials with negative Poisson's ratio: I. Microstructure and mechanical properties, J. Phys. D., Appl. Phys. 1989, 22, 1877-1882.
[13] K.E. Evans, and B.D. Caddock, "Microporous materials with negative Poisson's ratio: II. Mechanisms and interpretation", J. Phys. D., Appl. Phys. 1989, 22, 1883-1887.
[14] F. Homand-Etienne and R. Houpert, "Thermally induced microcracking in granites: characterization and analysis", Int. J. Rock Mech. Min. Sci & Geomech. Abstr. 26, 125-134, 1989.
[15] A. Nur and G. Simmons, "The effect of saturation on velocity in low porosity rocks", Earth and planetary science letters 1969, 7, 183-193.
[16] K. L. Alderson, and K. E. Evans, "The fabrication of microporous polyethylene having a negative Poisson's ratio", Polymer, 1992, in press.
[17] Lakes, R. S., "No contractile obligations", Nature, 1992, 358, 713-714.
[18] C.T. Herakovich, "Composite laminates with negative through-the -thickness Poisson's ratio", J. Composite Materials 1985, 18, 447-455.
[19] Tsai, S.W. and Hahn, H.T., Introduction to composite materials, Technomic, Lancaster PA 1980.
[20] M. Miki and Y. Morotsu, "The peculiar behavior of the Poisson's ratio of laminated fibrous composites", JSME International Journal, 1989, 32, 67-72.
[21] G. Milton, "Composite materials with Poisson's ratios close to -1", J. Mech. Phys. Solids, 1992, 40, 1105-1137.
[22] G. Simmons, and H. Wang, Single crystal elastic constants and calculated aggregate properties: a handbook, MIT Press, Cambridge, 2nd ed, 1971.
[23] A.E.H. Love, A Treatise on the Mathematical Theory of Elasticity, 4th ed, Dover, NY, 1944
[24] N. Bettenbouche, G. A. Saunders, E. F. Lambson, and W. Hönle, "The dependence of the elastic stiffness moduli and the Poisson ratio of natural iron pyrites FeS2 upon pressure and temperature", J. Phys. D., Appl. Phys. 1989, 22, 670-675.
[25] Y. Li, "The anisotropic behavior of Poisson's ratio, Young's modulus, and shear modulus in hexagonal materials", Phys. Status Solidi , 1976, 38, 171-175.
[26] D. J. Gunton and G. A. Saunders, "The Young's modulus and Poisson's ratio of arsenic, antimony, and bismuth", J. Materials Science, 1972, 7, 1061-1068.
[27] A. Y. Haeri, D. J. Weidner, and J. B. Parise, "Elasticity of [[alpha]]-cristobalite: a silicon dioxide with a negative Poisson's ratio", Science, 1992, 257, 650-652.
[28] A. M. Garber, "Pyrolytic materials for thermal protection systems", Aerospace Engineering 1963, 22, 126-137.
[29] M. Ya. Popereka and V.G. Balagurov, "Ferromagnetic films having a negative Poisson's ratio", Soviet Physics Solid State 1970, 11, 2938-2943.
[30] T. Hailing, G. A. Saunders, Y. K. Yogurtcu, H. Bach, and S. Methfessel, "Poisson's ratio limits and effects of hydrostatic pressure on the elastic behavior of Sm1-xYxS alloys in the intermediate valence state", J. Phys. C: Solid state Physics, 1984, 17, 4559-4573.
[31] H. Boppart, A. Treindl, and P. Wachter, "Phonon and elastic anomalies in intermediate valent TmxSe and TmSe1-yTey", in Valence Fluctuations in Solids, ed. L. M. Falicov, W. Hanke, and M. B. Maple, North Holland, 1981.
[32] S.Hirotsu, "Elastic anomaly near the critical point of volume phase transition in polymer gels", Macromolecules, 1990, 23, 903-905.
[33] J.H. Weiner, Statistical Mechanics of Elasticity, J. Wiley, NY, 1983.
[34] S. P. Timoshenko, History of Strength of Materials, Dover, NY, 1983.
[35] S. Burns, "Negative Poisson's ratio materials", Science, 1987, 238, 551.
[36] K.E. Evans, "Tensile network microstructures exhibiting negative Poisson's ratio", J. Phys. D., Appl. Phys., 1989, 22, 1870-1876.
[37] R.S. Lakes, "Experimental microelasticity of two porous solids", International Journal of Solids and Structures, 1986, 22, 55-63.
[38] R.S. Lakes, "Negative Poisson's ratio materials", Science, 238, (1987) 551.
[39] R.S. Lakes, "Deformation mechanisms of negative Poisson's ratio materials: structural aspects", J. Materials Science, 1991, 26, 2287-2292.
[40] K.W. Wojciechowski, "Two-dimensional isotropic system with a negative Poisson ratio", Physics Letters A, 1989, 137, 60-64.
[41] R.J. Bathurst and L. Rothenburg, "Note on a random isotropic granular material with negative Poisson's ratio", Int. J. Engng. Sci, 1988, 26, 373-383.
[42] L. Rothenburg, A. A. Berlin, and R.J. Bathurst, "Microstructure of isotropic materials with negative Poisson's ratio", Nature, 1991, 354, 470-472.
[43] C.P. Chen and R.S. Lakes, "Holographic study of conventional and negative Poisson's ratio metallic foams: elasticity, yield, and micro-deformation", J. Materials Science, 1991, 26, 5397-5402.
[44] E.D. Case, "The effect of microcracking upon the Poisson's ratio for brittle materials", Journal of Materials Science 1984, 19, 3702-3712.
[45] A. W. Lipsett and A. I. Beltzer, "Reexamination of dynamic problems of elasticity for negative Poisson's ratio", J. Acoust. Soc. Am 1988, 84, 2179-2186.
[46] A. Freedman, "The variation, with the Poisson's ratio, of Lamb modes in a free plate, I, general spectra", J. Sound and Vibration, 1990, 137, 209-230.
[47] R. S. Lakes, "Saint Venant end effects for materials with negative Poisson's ratios",
J. Applied Mechanics, 59, 744-746 1992.
[48] R. S. Lakes, "Design considerations for negative Poisson's ratio materials"
ASME Journal of Mechanical Design, 115, 696-700, 1993.
[49] J. B. Choi and R. S. Lakes, "Design of a fastener based on negative Poisson's ratio foam", Cellular Polymers, 1991, 10, 205-212.
[50] K. Evans, "Tailoring the negative Poisson's ratio", Chemistry and Industry 1990, Oct, 654-657.
[51] R. S. Lakes, "Polyhedron cell structure and method of making same" U.S. Patent #4,668,557, 26 May 1987.
[52] J. Cherfas, "Stretching the point", Science 1990, 247, 630.
[53] C.P. Chen, and R.S. Lakes, "Dynamic wave dispersion and loss properties of conventional and negative Poisson's ratio polymeric cellular materials", Cellular Polymers, 1989, 8, 343-359.
[54] Evans, K.E., Nkansah, M. A., Hutchinson, I. J., and Rogers, S. C., "Molecular network design", Nature , 1991, 353, 124.
Acknowledgment
Support of this research by the NASA/Boeing ATCAS program under contract
#NAS1-18889, and by a University Faculty Scholar Award is gratefully acknowledged.
Partial support by the ONR is also gratefully acknowledged.
Figures