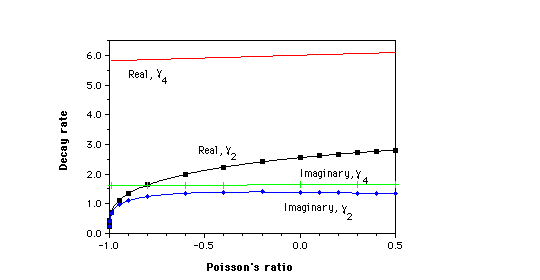
1. Decay constant [[gamma]]2 and [[gamma]]4 vs Poisson's ratio for end stress on a circular cylinder.
Saint-Venant end effects for materials with negative Poisson's ratios
Adapted from J. Applied Mechanics, 59, 744-746 (1992). Diagrams at bottom.
Download pdf
Preface
Novel materials are presented, which exhibit a negative Poisson's ratio. Such a material expands laterally when stretched, in contrast to ordinary materials. The original negative Poisson's ratio foam was developed by Rod Lakes. Later writers have called such materials anti-rubber, auxetic, or dilatational. End effects may be particularly pronounced when such materials attain extreme limits on Poisson's ratio or on nonlocal behavior, or if they have rigid elements connected by hinges.
Abstract
In this article we analyze Saint-Venant end effects for materials with negative Poisson's ratio. We present an example of slow decay of stress arising from self-equilibrated stress at the end of a circular cylinder of elastic material with a negative Poisson's ratio. By contrast a sandwich panel containing rigid face sheets and a compliant core exhibits no anomalous effects for negative Poisson's ratio, but exhibits slow stress decay for core Poisson's ratio approaching 0.5. In sandwich panels with stiff but not perfectly rigid face sheets, slow decay of stress is known to occur; a negative Poisson's ratio results in end stress decay which is faster than it would be otherwise.
1 Introduction
Recently, the invention of negative Poisson's ratio foams was reported by Lakes (1987a,b), and further developments by Friis et. al, (1988) and by Lakes(1991). Poisson's ratios as small as -0.7 were observed in polymer foams and values to -0.8 have been observed in metal foams. It is therefore of interest to re-examine some of those three dimensional stress distributions which depend on Poisson's ratio. In this article we consider stress fields which are relevant to Saint-Venant's principle. Saint-Venant's principle is important in the application of elasticity solutions in many practical situations in which boundary conditions are satisfied in the sense of resultants rather than pointwise. Research in the area of Saint-Venant's principle is reviewed by Horgan and Knowles (1983), Horgan (1989). It is now known that self equilibrated end stresses can decay slowly in highly anisotropic solids (Horgan, 1974, 1982, 1989; Choi and Horgan, 1977). We remark that
considerations of positive definite internal energy (hence stability) restrict the range of Poisson's ratio in linear isotropic elastic solids to -1 < [[nu]] < 1/2. Peculiarities are known to arise for Poisson's ratios approaching the upper limit 1/2, as in rubbery solids. In this article we explore a case of slow stress decay in isotropic solids with negative Poisson's ratios [[nu]], particularly for values approaching the lower limit -1.
2 The axisymmetric end problem for circular cylinders
Self equilibrated axisymmetric shear and normal tractions acting on the end surface of a right circular isotropic elastic cylinder give rise to stresses which decay exponentially along the length of the cylinder. An exact solution for the problem of end stress upon a circular cylinder with stress free lateral surfaces is given (Horvay and Mirabal, 1958) by the Love function (Little, 1973)
l = e-[[gamma]]z J0([[gamma]]r) + ([[gamma]]re-[[gamma]]zJ1([[gamma]]r) /2 (1-[[nu]]) +[[gamma]]J0([[gamma]]r)/J1([[gamma]]r)) (1)
in which r is a radial coordinate in units of the cylinder radius, z is a similarly normalized axial coordinate along the cylinder axis, and J0 and J1 are Bessel functions of order zero and one respectively. The construction of l in terms of spatial derivatives of the stresses results in satisfaction of the compatibility conditions and of one equilibrium equation; the second equilibrium equation is satisfied if l is required to be biharmonic (Little, 1973). An exact solution which satisfies the boundary conditions is obtained if [[gamma]] satisfies the eigenvalue equation
(J02([[gamma]]r) / J12([[gamma]]r)) - (2(1-[[nu]])/ [[gamma]]2)+1 = ([[gamma]]/ [[nu]]) = 0 (2)
Since the shear and normal stresses associated with these eigenvalues occur together, various orthogonalization and approximation schemes have been developed to obtain solutions for prescribed tractions on the end. For the purposes of this study it suffices to consider the real part of the lowest eigenvalue [[gamma]]2 since that determines the longest decay length L = 1/[[gamma]]2. We determined the eigenvalue by using a computer to generate contour plots of the real and imaginary parts of ([[gamma]]/[[nu]]) vs the real and imaginary parts of [[gamma]]. An approximate value of [[gamma]]2 was extracted from the intersection of the zero contours of Re(f([[gamma]],[[nu]])) and Im (([[gamma]] / [[nu]])), and a steepest descent approach was used to converge from this approximate value to [[gamma]]2. Results are shown in Figures 1 and 2. Fig. 1 also shows the next eigenvalue [[gamma]]4. The asymptotic behavior of [[gamma]]2 for [[nu]] ~ -1 is [[gamma]]2 [[proportional]] (1+[[nu]])^1/4 which is consistent with the slope of the curve in Fig. 2. Observe that as [[nu]] tends to its lower limit -1, [[gamma]]2 approaches zero, hence the decay length for the stresses goes to infinity. This result is physically reasonable since for [[nu]] ~ -1, the shear modulus G = 3B(1-2[[nu]])/2(1+[[nu]]) greatly exceeds the bulk modulus B, consequently a volume change over a large region of the cylinder is more energetically favorable than a large shear deformation localized near the end. In contrast, [[gamma]]4 did not exhibit much dependence on Poisson's ratio as shown in Fig. 1. [[gamma]]4 corresponds to a shear stress distribution which changes sign once vs r, in contrast to [[gamma]]2 in which the stress does not change sign. The result for [[nu]] ~ -1 was checked by performing a Taylor expansion approximation for the Bessel functions in Eq. 2, resulting in
[[gamma]]2 ~ (1+i) (8.7(1+[[nu]]))^1/4 (3)
which is consistent with the limiting behavior found above and shown in Fig. 2. In comparing the present results for [[gamma]]2 with those of Horvay and Mirabal (1958) we find excellent agreement (within the most significant figure quoted for the 'exact' value) for [[nu]] = 0.3, for which both an exact and an approximate value were presented in Horvay and Mirabal (1958), and good agreement with graphical values for [[nu]] > 0. However the approximate analysis in Horvay and Mirabal (1958) gives Re([[gamma]]2) = 2.2 for [[nu]] = -1, in contrast to a limiting value of zero in the present study. Moreover, inequalities based on energy considerations Knowles and Horgan (1969) yield a decay constant about a factor of two smaller than that given in Horvay and Mirabal (1958), at least for 0<=[[nu]]<=0.5. We conclude that the error in the variational approach in Horvay and Mirabal (1958) is not uniform in Poisson's ratio. The implications for other similar approximate analyses intended to cover the full range of elastic constants are obvious. Exact treatments of the cylinder end problem for prescribed end tractions have been presented in many articles. In some cases a restricted range of positive Poisson's ratio is assumed, but the main difficulty in the exact solutions is their complexity: the dependence of decay rate on Poisson's ratio is not at all obvious and can only be extracted with much labor.
2 The end problem for a sandwich panel
Sandwich panels consisting of stiff face sheets bonded to a low density core material are very useful in the aircraft industry and in other applications
requiring high stiffness per unit weight. End effects in sandwich structures have been examined by Choi and Horgan (1978) and results displayed for [[nu]] >= 0. We consider here some of the implications of [[nu]] < 0.
Limiting case: rigid face layers
The eigenvalue equation for the case of face sheets much stiffer than the core, for plane strain, is (Choi and Horgan, 1978)
4 - (2(1+[[nu]]) / (1-[[nu]]^2)) sin(2[[gamma]])+ 2[[gamma]] (2(1+[[nu]]) / (1-[[nu]]^2)) = 0 (4)
in which [[nu]] is the core Poisson's ratio. We compute the decay rate for the full range of Poisson's ratio and display the results in Fig. 3. In this case there is nothing unusual for [[nu]] -> -1, however(Choi and Horgan, 1978) for [[nu]] -> 0.5, the decay rate [[nu]] goes to zero (as [3(1 + 2[[nu]])/(3- 4[[nu]])]^1/2), consequently the decay length diverges. Practical sandwich panels incorporate as core anisotropic honeycombs or relatively stiff foam (with a Poisson's ratio of about 0.3). Use of negative Poisson's ratio foam as core is possible; no dramatic effect on Saint Venant's principle is anticipated for the sandwich geometry for perfectly rigid face sheets.
Stiff face layers
If the face layers are much stiffer than the core, but not perfectly rigid, new roots appear for the eigenvalue equation which were not anticipated in the above case (Choi and Horgan, 1978); for [[gamma]]<<1,
[[gamma]] ~ (5)
in which the subscripts 1 and 2 refer to the face and core materials respectively and f is the volume fraction of face material. Here, [[gamma]] becomes smaller and the decay length becomes larger as the face material becomes stiffer than the core material (Choi and Horgan, 1978): E1>> E2. This slow stress decay can, however, be mitigated by using a negative Poisson's ratio material for the core.
3 Discussion
Slow decay of end stress with respect to distance can arise from extreme values of the Poisson's ratio as well as from the geometry or anisotropy of the solid which had been known earlier. In some situations a negative Poisson's ratio results in slow stress decay; in other situations, more rapid stress decay. As for a general rule to discriminate these situations, we can only offer at this point the heuristic view that if a material can undergo either rapid stress decay via shear or slow stress decay via a volume change, the latter will be favored for negative Poisson's ratios approaching
the lower limit.
The effect of negative Poisson's ratio differs from the effect of anisotropy in the following ways. Anisotropy alters the rate of stress decay in a two dimensional strip (Choi and Horgan, 1977). In contrast, in an isotropic
two dimensional strip, Poisson's ratio has no effect on stress decay (Choi and Horgan, 1978). In an anisotropic strip, [[gamma]] ~ [[pi]][[radical]]GLT/EL
<<1 with L referring to the longitudinal direction and T to the transverse direction. In three dimensions, anisotropy can also give rise to slow stress
decay. In the isotropic three dimensional case, G/E =1/(2(1+[[nu]])) >>1 for [[nu]] -> -1, however for the circular cylinder considered above, [[gamma]] -> 0. There is no contradiction since the anisotropic relation was based on the assumptions ET/EL <<1, GLT/EL <<1, ET/GLT ~1 which are certainly
sensible for unidirectional fibrous composites but which do not permit passage to the isotropic limit.
As for physically realizable materials, we have achieved [[nu]] ~ -0.8 in cellular solids thus far; lower values are certainly possible. As for
the use of linear elasticity to describe materials with microstructure such as foams, foams can certainly be given large deformations which would require a nonlinear theory, however for sufficiently small strain, they behave linearly as do other materials. Some foams are described better by Cosserat elasticity (Lakes, 1986) rather than classical elasticity, however such effects depend on the cell size. Negative Poisson's ratio materials can be prepared with arbitrarily small cell size (Lakes, 1987a,b), and these materials would be classically elastic.
4 Conclusions
1. Slow decay of end stress occurs in circular cylinders of negative Poisson's ratio material.
2. In comparison, a variational determination of the decay rate had an error which was highly nonuniform in Poisson's ratio. Caution is recommended in the interpretation of such approximate analyses over a range in elastic constants.
3. The slow stress decay previously predicted for sandwich strips in plane deformation as a result of the geometry can be mitigated by use of a negative Poisson's ratio material for the core.
5 Acknowledgment
Support of this research by the NASA/Boeing ATCAS program under contract #NAS1-18889, and by a University Faculty Scholar Award to RSL is gratefully acknowledged. Partial support by the NSF is also gratefully acknowledged. I thank W. Drugan and M. Johnson of the University of Wisconsin for encouragement and discussions.
6 References
Choi, I. and Horgan, C. O., 1977,"Saint Venant's principle and end effects in anisotropic elasticity", J. Applied Mechanics , Vol. 44, pp. 424-430.
Choi, I. and Horgan, C. O., 1978, "Saint Venant end effects for plane deformation of sandwich strips", Int. J. Solids, Structures, Vol. 14, pp. 187-195.
Friis, E. A., Lakes, R. S. and Park, J. B., 1988, "Negative Poisson's ratio polymeric and metallic foams", J. Materials Sci., Vol. 23, 4406-4414.
Horgan, C. O., 1974, "The axisymmetric end problem for transversely isotropic circular cylinders", Int. J. Solids, Structures, Vol. 10, pp. 837-852.
Horgan, C. O., 1982,"Saint-Venant end effects in composites",J. Composite Materials Vol. 16,411-422.
Horgan, C. O., 1989,"Recent developments concerning Saint Venant's principle: an update", Appl. Mech. Rev., Vol. 42, 295-303.
Horgan, C. O. and Knowles, J. K., 1983, "Recent developments concerning Saint Venant's principle", Adv. Appl. Mech., (T Y Wu and J W Hutchinson, Eds) Academic, NY pp. 179-269.
Horvay, G. and Mirabal, J. A. , 1958, "The end problem of cylinders", J. Applied Mech., Vol. 25, 561-570.
Knowles, J. K. and Horgan, C. O., 1969, "On the exponential decay of stresses in circular elastic cylinders subject to self equilibrated loads", Int. J. Solids, Structures, Vol. 5, pp. 33-50.
Lakes, R.S., 1986, "Experimental microelasticity of two porous solids",
International Journal of Solids and Structures, Vol. 22 pp. 55-63 .
Lakes, R. S., 1987a,"Foam structures with a negative Poisson's ratio", Science Vol. 235, pp.1038-1040.
Lakes, R.S., 1987b, "Negative Poisson's ratio materials" , Science, Vol. 238 p. 551.
Lakes, R. S., 1991, "Deformation mechanisms in negative Poisson's ratio materials: structural aspects", J. Materials Science, Vol. 26, pp.2287-2292.
Little, R., 1973, Elasticity, Prentice Hall, NJ.
List of figures

1. Decay constant [[gamma]]2 and [[gamma]]4 vs Poisson's ratio for end stress on a circular cylinder.
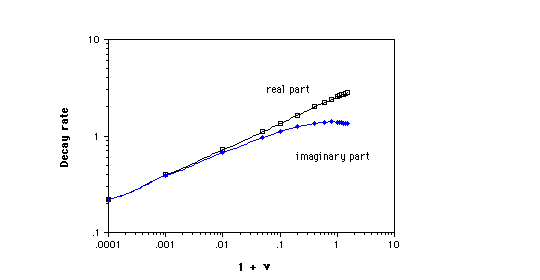
2. Decay constant [[gamma]]2 vs 1 + [[nu]] for end stress on a circular cylinder.
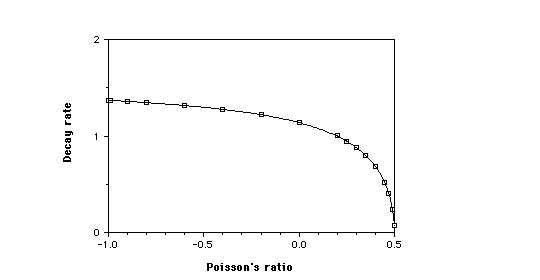
3. Decay constant [[gamma]] vs Poisson's ratio for end stress on a sandwich strip with perfectly rigid face sheets in plane strain.