Preface
Negative Poisson's ratio material expands laterally when stretched, in contrast to ordinary
materials. Negative Poisson's ratio foam was first developed by Rod
Lakes. Later writers have called such materials anti-rubber, auxetic, or dilatational.
Abstract
In this article we make use of the negative Poisson's ratio of recently developed cellular solids in the design of a press-fit fastener. Insertion of the fastener is facilitated by the lateral contraction which negative Poisson's ratio materials exhibit under compression. Removal of the fastener is resisted by the corresponding elastic expansion under tension. Download a pdf of this article.
1 Introduction
The invention of a new class of negative Poisson's ratio foams has been recently reported [1-3]. These are in contrast to most ordinary materials, including most cellular solids, which have Poisson's ratios near 0.3. Metallic and polymeric foams were transformed so that their cellular micro- structure became re-entrant, i.e. with inwardly protruding cell ribs. Re-entrant foams exhibited negative Poisson's ratios as well as greater resilience than conventional foams. The polymer foams exhibited negative Poisson's ratios as small as -0.7, and metal foams exhibited values to -0.8. There are other structural possibilities for achieving negative Poisson's ratios, and these are reviewed in [4].
Applications of materials with negative Poisson's ratios may be envisaged (i) based on the Poisson's ratio, (ii) based on the superior toughness, resilience, and tear resistance which has been observed in these materials, and (iii) based on the acoustic properties associated with the vibration of ribs in the material. The Poisson's ratio influences deformation kinematics in ways which may be useful, and it influences the distribution of stresses. For example, stress concentration factors are reduced in some situations, increased in others, when Poisson's ratio is negative. Materials with negative Poisson's ratios can quantitatively improve the performance of applications such as wrestling mats
and cores for sandwich panels; these will be described elsewhere. We consider here the design of a press-fit fastener based on a negative Poisson's ratio material, in which the Poisson's ratio itself is relevant.
2.
Design of the fastener
2.1
Basic concept; consideration of material nonlinearity
The fastener consists of a hollow circular cylindrical core, made of negative Poisson's ratio material, and a socket with a corresponding cylindrical hole. The fastener is made bigger than the hole by a tolerance t in the radial dimension. As it is inserted, the longitudinal force of insertion causes its diameter (transverse dimension) to become smaller by virtue of the negative Poisson's ratio. With sufficient force, the core diameter becomes equal to the hole diameter and the core can be inserted into the hole. Axial force applied to remove the fastener causes the core to expand laterally, generating an increased frictional force which resists removal.
All negative Poisson's ratio materials studied to date exhibit a nonlinear relationship between the Poisson's ratio
n;
and
the longitudinal strain
e;
z
Poisson's ratio is represented by a Greek nu and strain by a Greek epsilon. If your browser does not handle the font face tag properly, the Greek letters may not show up. If that is a problem, use the pdf version.
For the purpose of analysis, the observed nonlinear dependence on strain (Fig.1) is approximated as a quadratic in the interval -b less than
e
zless than b.
The parameters a and b describe the form of nonlinearity and are to be obtained
from experiment.
n
=
ez2
(a/b
2)
- a.
(1)
Poisson's ratio is defined as
n
=
-
er/ez,
with
er
as
the radial strain. So,
er
=
-
nez
= - (a/b
2)
ez3
+
a
ez . (2)
The
cubic relationship between radial strain and longitudinal strain exhibits
relative maxima in the magnitude of the radial displacement at the surface for
values of
ez
defined
as plus or minus
c;
with c = plus or minus b/square root3. Even though the material has a negative
Poisson's ratio for strains from
ez=
0 to c to b, the radial displacement decreases for
ez
greater than c. The radial component of displacement u
r
is
given by
(dur/dr)
|umax
= - (ac
3/b2)
+
ac,
(3)
with
u
max
=
(2ab/3square root3)(r
o
-r
i).
The
maximum radial displacement must be greater than the tolerance t, consequently,
in view of the assumed material nonlinearity,
(ro
-r
i)
≥ (3tsquare root3/2ab) .
(4)
2.2
Forces of insertion and removal
Now
consider, in an elementary vein, the forces associated with insertion and
removal of the fastener core, which is assumed to have a tangent Young's
modulus of E
1
at the maximum longitudinal strain occurring during insertion. The force F
i
required
to insert the fastener will be the force which causes sufficient longitudinal
strain
ez
to
achieve a radial contraction equal to t. So,
F
i
=
p(ro2
-
r
i2)
E
1
ez
(5)
But
er
=
-
nez
= (t/(r
o
-r
i))
.
(6)
So
the insertion force is
Fi
=
-
p
(r
o
+
r
i
)
E
1
(t/
n)
(7)
The
force
Frm
required
for removal of the fastener arises from friction with the cylindrical hole. The
friction force is distributed over the region of contact of length h, and an
increment of this force over region dz is
dF
rm
= 2
p
(r
o-
t)
msr(z)dz
(8)
in
which m is the coefficient of friction
,
sr
is
the
radial
stress
The
radial
stress
sr
is
obtained via an (approximate) Hookean analysis.
sr(z)
=
E2
er(z)
=
E
2
(nez(z)-
t/(r
o
-
r
i))
(9)
in
which E
2
is
the tangential modulus as Young's modulus at a certain
ez
Therefore,
we have the following integral
Frm
=
2π
(r
o-
t)
m;
E2Integral( lower 0, upper h,(nez(z)-
t/(r
o
- r
i)))dz
(10)
The
maximum force for removal of the fastener is limited by the strain
ez(z)
= c =b/square root3 which gives the maximum contact force. If the fastener material
is sufficiently strong, the maximum removal force is:
Frm,max
=
m;E22p
(r
o-
t)h [
n(b/square root3)
- (t/r
o
- r
i)
]
(11)
Observe
that since
n
is
negative, the first term in the [] brackets also contributes to the removal
force in the same sense as the effect of preparing an oversize core, as
embodied by the second term. The removal force depends on both the Poisson's
ratio
n
and
on the measure b of nonlinearity. If b could be made larger, ie a Poisson's
ratio less dependent on strain, the removal force would be larger.
2.2
Specific example: copper re-entrant foam
Copper
foam is chosen since it is relatively stiff (E = 300 MPa), and is ductile
enough to be easy to process. For copper re-entrant foam with an initial
relative density of 0.1 and a permanent volumetric compression ratio of 2.13
and at a strain of 0.001,
n
=
-0.8 plus or minus 0.05. The Poisson's ratio is assumed to be negative up to a
strain of 0.2 [3]. Therefore constants above are chosen as a = 0.8 and b = 0.2.
Consider
first the case of a small radial tolerance t=0.01mm; let h=30 mm and r
o=10
mm. Then from Eq. 4, r
i
less than 9.8 mm; we choose r
i
= 3 mm. We obtain
ez
= 0.18% as the strain required for insertion. The unlubricated friction
coefficient of copper on steel is 0.22 [5]. The tangential Young's moduli E
1,E2
at longitudinal strains of 0.18% and 0.2% are both about 30 MPa for copper
foam[3]. Therefore, the force required to insert this fastener is F
i
= 15 N; and to remove it, F
r
= 112 N.
Consider
now the case of a larger radial tolerance t=0.05mm. We calculate r
i
less than 8.8 mm, and choose r
i=5
mm. For this case
ez
= 0.025 is the insertion strain. With E
1,E2
of 40 MPa and 10 MPa respectively and corresponding Poisson's ratios of -0.79
and -0.51 [3] at strains of 0.025 and 0.12, the insertion force is calculated
as F
i
= 119 N and the removal force is F
r
= 211 N. In this case the material nonlinearity limits the removal force.
3 Experimental
Materials and Methods
In
this experiment, the performance of a fastener made of re-entrant negative
Poisson's ratio copper foam was evaluated by a simple push-pull test.
A
re-entrant copper foam specimen was prepared as a core. The material had an
initial relative density (density of foam divided by density of solid copper)
of 0.03, a permanent volumetric compression ratio of 2.5, and a final Young's
modulus of 55 MPa. It was machined into a hollow cylindrical form (outside
diameter 18.24 mm, inside diameter 6.35 mm, length 55 mm) and polished with
abrasive grit as fine as No. 1000. The socket was machined from steel with a
hole of diameter 80 m;m less than the outside diameter of the cylindrical
core, so that t = 40 m;m; the hole length was 25.5 mm. The machining
tolerance was 13 m;m. The fastener was annealed at 500 °C for 1 hr to
minimize effects of cold work. The end of the core not inserted in the socket
was embedded 20 mm deep in polymethyl methacrylate (PMMA) to form a grip; PMMA
is much more rigid (E = 3 GPa) than the copper foam (E = 55 MPa).
The
fastener was tested using a servohydraulic testing machine with a 2.5 kN load
cell (MTS Corp.) to insert and remove the fastener core while monitoring the
associated forces. Alignment for insertion was achieved by placing a low
friction (Teflon) tape between the socket and the machine platen. For removal
of the fastener core, the socket was fixed to the platen. Experiments were
performed at a constant displacement rate of 0.1 mm/sec.
4 Experimental
Results
Figure
2 shows the observed dependence of load on displacement for insertion and for
removal of the fastener. During insertion, the load-displacement graph showed
an initial sharp increase in load and then a more gradual increase in load
until the maximum displacement was reached. The load-displacement curve showed
a small fluctuation of up to 2.5N in load. This suggests a stick-slip
frictional force or possibly a slight amount of crushing of the surface cell
ribs in the core.
The
fastener broke at a displacement of 2.8 mm and a load of 160N during the
pull-out process. The fracture surface was in the body of the core, away from
the socket and embedded grip ends. Moreover, the fracture surface was rough.
The experimental results for maximum insertion and removal force were 70N and
160N, respectively. In comparison, the theoretical predictions were 60 N and
210 N, respectively. The observed maximum removal force was limited by the
strength of the copper foam, not by friction, so it is reasonable that the
observed removal force was less than the theoretical maximum friction force.
5 Discussion
and conclusions
Foamed
material is considerably less stiff and strong than the same material in solid
form. Therefore, the strength of a fastener based on negative Poisson's ratio
cellular solids will be less than that of a corresponding solid screw of the
same diameter. In the present study, a foam containing only 0.03 x 2.5 or 7.5%
solid material was used; a denser foam material would provide greater strength.
The difference in strength could be compensated for by designing a fastener of
larger diameter than would otherwise be used. The advantage of a negative
Poisson's ratio fastener is the simplicity of the press-fit insertion. The
example presented here of copper foam was chosen since it was readily
available, is stiffer (E = 55 MPa) than the elastomeric polymer foams
previously examined ( E = 70 kPa) and its ductility facilitates
transformation into a re-entrant structure. Fasteners based on stiff polymer
foam are possible as well. Materials with negative Poisson's ratios of
considerably higher stiffness and strength than those considered here are
possible based on the concept of re-entrant cells [1,3] as well as other
structures[4], so the design presented here is intended as illustrative rather
than optimal.
We
conclude that press-fit type fasteners may be designed using negative Poisson's
ratio materials, and that such fasteners perform in a manner consistent with a
simple analysis.
6 References
1. Lakes,
R. S., "Foam structures with a negative Poisson's ratio", 1987,ScienceVol. 235,1038-1040.
2. Lakes,
R. S., "Negative Poisson's ratio materials",
Science,
1987, Vol. 238, 551 (1987).
3. Friis,E.
A., Lakes, R. S. and Park, J. B., "Negative Poisson's ratio polymeric and
metallic foams", J. Materials Sci. ,1988, Vol. 23, 4406-4414.
4. Lakes,
R. S., "Deformation mechanisms in materials with negative Poisson's ratios",
J.
Materials Sci.
,
1991, 26, 2287-2292 (1991).
5.
E. P. Bowden, D. Tabor,
The friction and Lubrication of solids,
Oxford University Press, 1950, pp322-323
List of figures

Fig. 1 Poisson's ratio vs longitudinal strain for re-entrant foam.
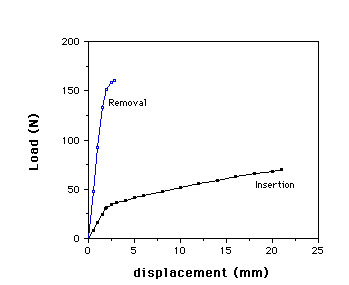
Fig. 2 Load vs displacement for experimental insertion and removal of fastener
core.
Top

