

Preface
Novel materials are presented, which exhibit a negative Poisson's ratio. Such a material expands laterally when stretched, in contrast to ordinary materials. The original negative Poisson's ratio foam was developed by Rod Lakes. Later writers have called such materials anti-rubber, auxetic, or dilatational. This is the first two-dimensional lattice metamaterial that is chiral; we did not call it by such a name.
This honeycomb or lattice was first introduced in 1991 in the context of causal deformation mechanisms for negative Poisson's ratio: Deformation mechanisms in negative Poisson's ratio materials: structural aspects, J. Materials Science, 26, 2287-2292 (1991).
Abstract
A theoretical and experimental investigation is conducted of a two-dimensionally chiral or noncentrosymmetric honeycomb. The honeycomb exhibits a Poisson's ratio of -1 for deformations in-plane. This Poisson's ratio is maintained over a significant range of strain, in contrast to the variation with strain seen in known negative Poisson's ratio materials.
1. Introduction
Cellular solids are used widely in a variety of engineering applications. In particular, honeycomb cell structures are very prevalent. The continuing desire for stronger, lighter weight, structural materials for use in aerospace and aircraft applications has made these industries the traditional leaders in the development of honeycomb structures for technological use. However, improved manufacturing processes have made these unique composite materials more affordable and viable for other industries.
Continuing interest in such structures has seen the birth of the next generation of unusual cellular solids. Much interest has centered around the recent discovery of re-entrant structures. These are unique honeycombs and foams which exhibit negative Poisson's ratios. The allowable range of Poisson's ratio in three dimensional isotropic solids is from -1 to one half [1]. Most common materials have a Poisson's ratio close to one third, however rubbery materials have values approaching one half; they readily undergo shear deformations, governed by the shear modulus G but resist volumetric (bulk) deformation governed by the bulk modulus K, so G << K. Although textbooks can still be found which categorically state that Poisson's ratios less than zero are unknown, there are in fact a number of examples of negative Poisson's ratio solids as described below. Such solids become fatter in cross section when stretched. A solid with [[nu]] ~ -1 would be the opposite of rubber: difficult to shear but easy to deform volumetrically: G >> K.
Two dimensional honeycombs with regular hexagonal cells (Fig. 1a) exhibit a Poisson's ratio of +1 in the honeycomb plane; the out-of-plane properties differ due to anisotropy. The cell walls have 120 deg. angles between walls and all walls must be of equal thickness and composition. In contrast honeycombs with inverted cells (Fig. 1b) give rise to negative Poisson's ratios in the honeycomb plane [2-5]. Analysis of deformation of these honeycombs [2,3,5,6] allows prediction of the Young's modulus and Poisson's ratio. Honeycombs are sufficiently simple that the Poisson effect can be easily visualized. Structures of the above type require some form of individual assembly. Foam materials with a negative Poisson's ratio as small as -0.7 were developed [7] in which an inverted or re-entrant cell structure was achieved by isotropic permanent volumetric compression of a conventional foam, resulting in microbuckling of the cell ribs. Polymer foams which exhibit a softening point [7,8], ductile metallic foams [7,8,9], and thermosetting polymer foams [8,10] can be prepared with a negative Poisson's ratio; [[nu]] ~ -0.8 can be attained in copper foam. The negative Poisson's ratio occurs over a range of strain [8,9,10] and that range is larger in the polymer than in the metal foams. In the above structures and materials, the negative Poisson's ratio arises from the unfolding of the re-entrant cells, and isotropy can be achieved along with the negative Poisson's ratio.
Other negative Poisson's ratio structures include the hinged frameworks of Almgren [11] and the linked structures of Evans [12]. Aside from the foams [7] developed by one of the authors, the only known isotropic negative Poisson's ratio material is an aggregate of crystals of [[alpha]]-cristobalite [13].
This article deals with a negative Poisson's ratio honeycomb [14] in which the negative Poisson's ratio is achieved by an unrolling action as was first suggested in [15]. The honeycomb is two-dimensionally chiral and has hexagonal symmetry. These may also be called chiral lattices or two dimensional auxetic honeycomb.
2. Materials and methods
The honeycomb structure shown in Fig. 2 is composed of circular elements or nodes of equal radius r joined by straight ligaments or ribs of equal length L. The ligaments are constrained to be tangential to the nodes. The angle between adjacent ligaments is equal to sixty degrees. The honeycomb simultaneously possesses both hexagonal symmetry and a two-dimensional chiral symmetry (or "handedness"). Structures exhibiting hexagonal symmetry are mechanically isotropic in-plane. Experiments discussed later confirm isotropy in Poisson's ratio. A commercially available polystyrene, (Evergreen Scale Models, Inc.) was used in the fabrication of a model honeycomb. In-plane Poisson's ratios [[nu]]12 and [[nu]]21 were determined as functions of axial strain for the honeycomb.
For this honeycomb structure, variations in three principal geometrical quantities are possible. First, the cell wall thickness t which was set at 0.25 mm. The node radius r was set at 6.35 mm. Finally the ratio R/r of the distance R between the centers of adjacent (ligament-joined) nodes and r was set at 5.0 for this model. All three quantities were selected with the following criteria in mind: to conform to available material dimensions, to promote ease of model construction, to allow adequate distances and stiffness for realistic and measurable behavior, and to achieve sufficiently low relative density that rib or ligament bending would dominate. In accordance with this last criterion, the wall thickness of the nodes was made 1.25 mm to allow for rigid body behavior of the nodes in comparison with the ligaments. Overall dimensions for the model, which contained 105 nodes, were approximately 305 mm x 355 mm.
This model structure was hand-built by first making a wooden jig which located the circular nodes. The nodes were cut to the proper depth of 10 mm from uniform annulus stock polystyrene (1.25 mm wall thickness) and placed on the jig. Ligaments were cut from uniform sheet stock polystyrene (0.25 mm thickness) to the correct width for depth and calculated length, L. The ligaments were aligned in position and welded to the nodes by brushing the joints with a solvent for polystyrene, methyl ethyl ketone (Testors reg. Plastic Cement no. 3502).
The entire model was placed on top of a high-quality photocopier and uniformly loaded in compression first in the X1 then in the X2 directions using a movable, rectangular frame. Displacements in both directions were recorded xerographically from the motion of targets placed on the model. Measurements of displacements were used to calculate the two Poisson's ratios. Resolution of all length measurements was limited to +/- 0.25 mm of the actual value. These results are presented and discussed in [[section]]4.
3. Analysis
3.1 Geometry and unit cell identification
In the following, expressions for the theoretical predictions for the Poisson's ratios [[nu]] 12 and [[nu]] 21 as well as for the corresponding Young's moduli E1 and E2 are developed. We remark that a two-dimensional structure has four independent elastic constants described by the Young's moduli E 1 and
E 2, a shear modulus G12, and Poisson's ratios [[nu]]12 and [[nu]]21. The reciprocal relation links the four constants of interest in this study as follows:
E1[[nu]]21 = E2[[nu]]12 (1)
As noted by Gibson and Ashby [6], the mechanism which dominates the linear elastic deformation of honeycombs is that of bending of the cell walls. The approach to determining the mechanical behavior for the overall honeycomb structure begins with the identification of the unit cell structure (the smallest, repeatable, oriented, structural unit). The geometry of this honeycomb is unusual, and the corresponding unit cell geometry is equally so. To visualize the unit cell represented by the heavier lines in Figure 3, the honeycomb is viewed as a lattice of many such cells with the aforementioned nodes comprising circular, interstitial spaces between adjacent cells.
Referring to Figure 3, the X1- axis passes through the centers of the described arcs along the major axis of the cell. The X2- axis passes through the corresponding points along the minor axis.
The necessary geometric parameters are described by the following relations:
sin [[theta]] = ((R/2)/R) => [[theta]] = 30 deg. (2)
sin [[beta]] = (2r/R) (3)
tan [[beta]] = (2r/L) (4)
Regardless of configuration, the angle between adjacent ligaments and adjacent node centers is constant and equal to 2[[theta]] = 60 degrees.
3.2 Linear elastic deformation mechanism
Analysis of the mechanism of cell wall bending as the primary influence upon in-plane moduli and Poisson's ratios for deformation of hexagonal cell honeycombs is presented by Gibson and Ashby [6]. In the case of the novel honeycomb described here, the same method is equally valid; hence, it is employed in a similar manner. However, owing to the unique structure of this honeycomb, some distinctions arise with regard to how the loads are transferred to the cell walls and how their deflections, in turn, cause the linear displacement within the cells.
In the initial, undeformed state before load application, the ligaments are straight (undeformed). Referring to Fig. 4, a uniaxial stress, [[sigma]]1 or [[sigma]]2, is applied to the cell along X1 or X2; as a consequence of this, a torque T results in bending of the ligaments into a sigmoid shape, and rotation of the nodes as described below. Both the ligament bending and the equal rotation of all nodes is visible experimentally in the deformation of the model. The ligaments remain rigidly tangent to the node, therefore the deformation is constrained to correspond to a change of area without change of shape. Deformations due to axial compression and shear within the ligament can be neglected so long as the ligaments are sufficiently slender, hence the relative density of the structure is kept below a critical value. In their general analysis of honeycombs, Gibson and Ashby suggest this value to be [[rho]] /[[rho]] s ~ 0.29, with [[rho]] as the honeycomb density and [[rho]] s as the density of the solid from which it is made.
When ligament AB is loaded it bends but the ligament does not rotate, so the angle between AB and the X1 (or any other fixed axis) remains constant. For very large deformations (not treated here), the length of AB will contract without any rotation. This effect has been verified empirically. The circular nodes do rotate since the motion of the ligament end is tangent to the circle.
The orthogonal deformations of the honeycomb result from the displacement of the node centers. The angular deflection [[phi]] of beam AB measured at its endpoints coincides with the nodes' rotation through the same angle, [[phi]] . This is due to the constraint that the slope of AB, at A or B, remains tangent to the node. So, in order to maintain [[phi]] and [[theta]], the ligaments must "wind" onto the nodes. This results in a displacement of adjacent nodes along the direction of R. The effective displacement of each node, is as if it were rolling along R.
Referring to Figure 4, the deformation, e , of the cell is the same for both nodes C and D and is related to the angular deflection [[phi]] of AB by
e = r sin [[phi]]
e1 = r[[phi]] cos [[theta]] (5)
e2 = r[[phi]] sin [[theta]]
in which, for small deflections, rsin[[phi]] ~ r[[phi]] and [[theta]] = 30deg..
3.3 Prediction of Poisson's ratios and in-plane moduli.
The deflection of any arbitrary ligament in the honeycomb is equivalent to that of AB due to a common load configuration for each. This deflection can be analyzed using standard beam theory [16] by modeling AB as a beam of thickness t , width d , length L , and Young's modulus Es (for the solid, in this case polystyrene). The standard result for the deflection is, with I = (1/12) t3d.
[[phi]] = (TL/6EsI) , or T = (Est3d/2L) [[phi]] (6)
The strains are, from Eq. (5):
[[epsilon]]1 = (e1/(0.866)R) = (0.866r[[phi]]/0.866R)
= [[phi]](r/R) (7)
[[epsilon]]2 = (e1/(0.5)R) = (0.5r[[phi]]/0.5R) = [[phi]](r/R) 8)
Poisson's ratios are calculated as follows for loading in both directions:
(9)
(10)
Young's modulus may be calculated via an energy approach. The internal energy U for the rib is
U = Integral (,,T d[[phi]]) (11)
Incorporating Eq. (6) and (7), and recognizing a torque is applied at each end,
Urib = 2 (Est3d/4L)[[phi]]2 = 2 (Est3d/4L) (R2 / r2 ) [[epsilon]]2 (12)
A cell contains three ribs each of which is shared with an adjacent cell, so the energy for one cell is 3/2 that of a single rib.
In the continuum view, with V as the volume,
Ucm = integral (,,[[sigma]] d[[epsilon]]) = V[[currency]]E[[epsilon]]2 (13)
For a single triangular cell, V = R2 F(R(3),2) d, so for that volume,
Ucm = sqrt (R(3)/4) Ed[[epsilon]]2 (13)
Equating the energies for one cell in the structural and continuum views,
E = Es Root(3) (t3/L3) F(L2/r2). (14)
The Young's moduli for loading in different directions must be equal owing to the kinematical constraint that the ligaments remain tangent to the nodes. For comparison, Gibson and Ashby obtain a similar dependence F(t3,L3) in honeycombs of conventional structure.
Applying the reciprocal theorem (Eq. 1) verifies that
E1[[nu]]21 = E2[[nu]]12 (15)
The fact that E1 = E2 and [[nu]]21 = [[nu]]12 suggest the mechanical symmetry of the honeycomb to be cubic or higher. As for structural symmetry, the honeycomb structure is invariant to 60 deg. rotations and 120 deg. rotations, but it is not invariant to inversions. As for directional anisotropy, we remark that structural invariance to 60 deg. rotations (hexagonal symmetry) gives rise to a mechanical condition of transverse isotropy, that is, isotropy in-plane [17]. Young's modulus of a hexagonal material is independent of direction in the plane normal to the hexagonal symmetry axis [18]. The present results are consistent with this symmetry argument. We remark the Gibson and Ashby suggest that certain types of triangular honeycomb are anisotropic in-plane, however based on established symmetry considerations, we expect that these were not perfectly symmetric.
The lack of inversion symmetry constitutes a chiral anisotropy, which is entirely distinct from directional anisotropy. Chirality has no effect on the classical elastic properties of a material. To demonstrate this, consider the tensorial Hooke's law
[[sigma]]ij= Cijkl [[epsilon]]kl, (16)
in which [[sigma]]ij is stress, [[epsilon]]kl is strain and C is the elastic modulus tensor.
The transformation law for the modulus tensor under coordinate changes is
Cijkl ' = aimajnakoaln Cmnop. (17)
For an inversion, the transformation matrix is just the negative of a Kronecker delta
a im = - d im. (18)
So the classical elastic modulus tensor is unchanged by chirality:
Cijkl ' = (-1)4 Cijkl = Cijkl. (19)
Some materials behave as generalized continua [19] which allow more freedom than classical elasticity. For example, Cosserat elasticity has a characteristic length scale. The non-classical behavior is influenced by chirality [20]. Effects of this type are absent in the current analytical and experimental work since they do not occur in the absence of strain gradients or gradients in rotation of micro-elements.
4. Experimental results and discussion
Experimental results for Poisson's ratio vs strain are shown in Fig. 5 and 6. Note the expanded scale in Poisson's ratio. The error bars represent inaccuracies due to the measurement resolution. Resolution error was dominant and was therefore used instead of error due to statistical considerations. As would be expected, the measurement error decreases as the strains increase. Results are consistent with the theoretical Poisson's ratio of -1, within the uncertainties involved. Poisson's ratio showed no obvious dependence upon strain, in agreement with theory. The theory based on cell wall bending provides a good approximation for both in-plane Poisson's ratios even at relatively high strains (up to ~ 0.2). However at sufficiently large strain, we expect that the assumptions of elementary beam theory used in the analysis would be problematical.
The circular nodes were observed to rotate as the honeycomb was deformed. Rotational degrees of freedom in solids are known analytically [19], and unusual effects can occur in three-dimensionally chiral materials with such freedom [20]. We remark that a chiral molecular structure consisting of 'rigid hexamers' and with a negative Poisson's ratio has been suggested [21]. Moreover in the present honeycomb, as the nodes rotated, the ligaments were observed to bend, as anticipated in the analysis. Ligament deformation was less regular at the edges, and the ligaments were not always tangent to their nodes at the specimen edges; under sufficient deformation these ligaments appeared to buckle. This is not surprising since the biaxial strain and state in the analysis cannot be sustained at the boundaries. The honeycomb was observed to recover fully to its original dimensions following strains of up to 25%.
The constancy of Poisson's ratio vs strain over a significant range of strain is unusual and differs from the behavior of other materials and structures. For example, Fig. 7 shows the behavior of re-entrant honeycomb with inverted hexagonal cells based on the analysis of Gibson and Ashby [6], and also an experimental curve for re-entrant copper foam [9]. The constancy of [[nu]] in the present honeycomb is due to the ability of the cells to "wind" in upon themselves during compression. In contrast, the other materials with a negative Poisson's ratio exhibit a substantial nonlinearity since deformation changes the angles between structural elements; these angles govern the Poisson's ratio. Young's moduli of chiral honeycomb depend upon the L/r ratio, hence the R/r ratio; the bending or buckling behavior of the ligaments, hence the strain ranges for which linear elastic theory will apply, can be expected to depend on this ratio.
Foams have three dimensional micro-structures, in contrast to honeycombs in which the relevant structural features are confined to two dimensions. We may envisage the possibility of three dimensional chiral micro-structures which deform via a mechanism similar to that which governs the present honeycomb, and which give rise to extremal Poisson's ratios over a wide range of strain.
5. Conclusions
1 Analysis based on ligament bending in the chiral honeycomb (or chiral lattice) predicts [[nu]] = -1 independent of strain, in two orthogonal directions.
2 Experimental determination of Poisson's ratio [[nu]] yields results consistent with [[nu]] = -1 independent of strain.
References
1. Y. C. Fung, Foundation of Solid Mechanics , Prentice-Hall, Englewood, NJ, 1968 p.353.
2. G. S. Schajer and C. I. Robertson, Mechanical behaviour of cellular structures, project report, Pembroke College, Cambridge University, 1974.
3. L. J. Gibson, M. F. Ashby, G. S. Schajer, and C. I. Robertson, The mechanics of two dimensional cellular solids, Proc. Royal Society London, A382, 25-42 (1982).
4. A.G. Kolpakov, On the determination of the averaged moduli of elastic gridworks, Prikl. Mat. Mekh, 59, 969-977 (1985).
5. T. L. Warren, Negative Poisson's ratio in a transversely isotropic foam structure, J. Appl. Physics, 67, 7591-7594 (1990).
6. L.J. Gibson and M. Ashby, Cellular solids, Pergamon, Oxford,(1988).
7. R. S. Lakes, Foam structures with a negative Poisson's ratio, Science , 235 1038-1040 (1987).
8. E. A. Friis, R. S. Lakes, and J. B. Park, Negative Poisson's ratio polymeric and metallic materials, Journal of Materials Science, 23 4406-4414 (1988).
9. J. B. Choi and R. S. Lakes, Nonlinear properties of metallic cellular materials with a negative Poisson's ratio, J. Materials Science, 27, 5373-5381 (1992).
10. J. B. Choi and R. S. Lakes, " Nonlinear properties of polymer cellular materials with a negative Poisson's ratio", J. Materials Science, 27, 4678-4684 (1992).
11. R. F. Almgren, "An isotropic three dimensional structure with Poisson's ratio = -1", J. Elasticity, 15, 427-430 (1985).
12. K.E. Evans, "Tensile network microstructures exhibiting negative Poisson's ratio", J. Phys. D., Appl. Phys. 22, 1870-1876 (1989).
13. A. Y. Haeri, D. J. Weidner, and J. B. Parise, "Elasticity of [[alpha]]-cristobalite: a silicon dioxide with a negative Poisson's ratio", Science, 257, 650-652 (1992).
14. D. Prall, Two-dimensional analysis of selected linear elastic properties for a novel honeycomb, project report, Department of Biomedical Engineering, University of Iowa, (1993).
15. R.S. Lakes, Deformation mechanisms of negative Poisson's ratio materials: structural aspects, J. Materials Science, 26, 2287-2292 (1991).
16. S.P. Timoshenko, Strength of materials part 1, elementary theory and problems (3rd ed.). New York: Van Nostrand, (1955).
17. B.D. Agarwal and L. J. Broutman, Analysis and performance of fiber composites, J. Wiley, New York, (1980).
18. J. F. Nye, Physical properties of crystals, Oxford University Press, Oxford, (1957).
19. R. D. Mindlin, Stress functions for a Cosserat continuum, Int. J. Solids and Structures 1, 265-271, (1965).
20. R. S. Lakes and R. L. Benedict, Noncentrosymmetry in micropolar elasticity. International Journal of Engineering Science, 29, 1161-1167, (1982).
21. K.W. Wojciechowski, "Two-dimensional isotropic system with a negative
Poisson ratio", Physics Letters A, 137, 60-64 , (1989).
List of figures
download pdf of this article.1 (a) Honeycomb with regular hexagonal cells
(b) Re-entrant honeycomb.
2 Two-dimensional chiral honeycomb structure.
(a) 
(b) Photograph of deformed honeycomb- see paper article
3 Geometry of the unit cell. Inset: load P and torque T as they act upon a ligament and a node.
4 Deformation of a ligament. Top: kinematics of the deformation. Bottom: free-body diagram of a ligament.
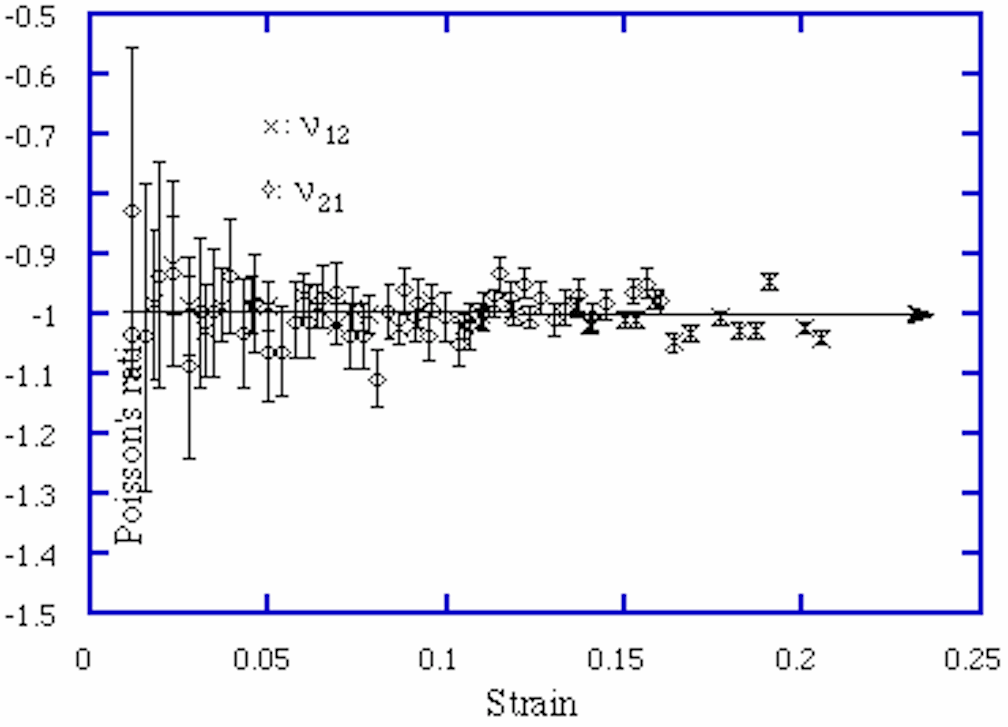
5 Experimental Poisson's ratio [[nu]] vs axial compressive strain of chiral honeycomb.
x: [[nu]]12 for loading along x1.
[[lozenge]]: [[nu]]21 for loading along x2.
Theoretical curve, [[nu]] = -1.
6 strain dependence
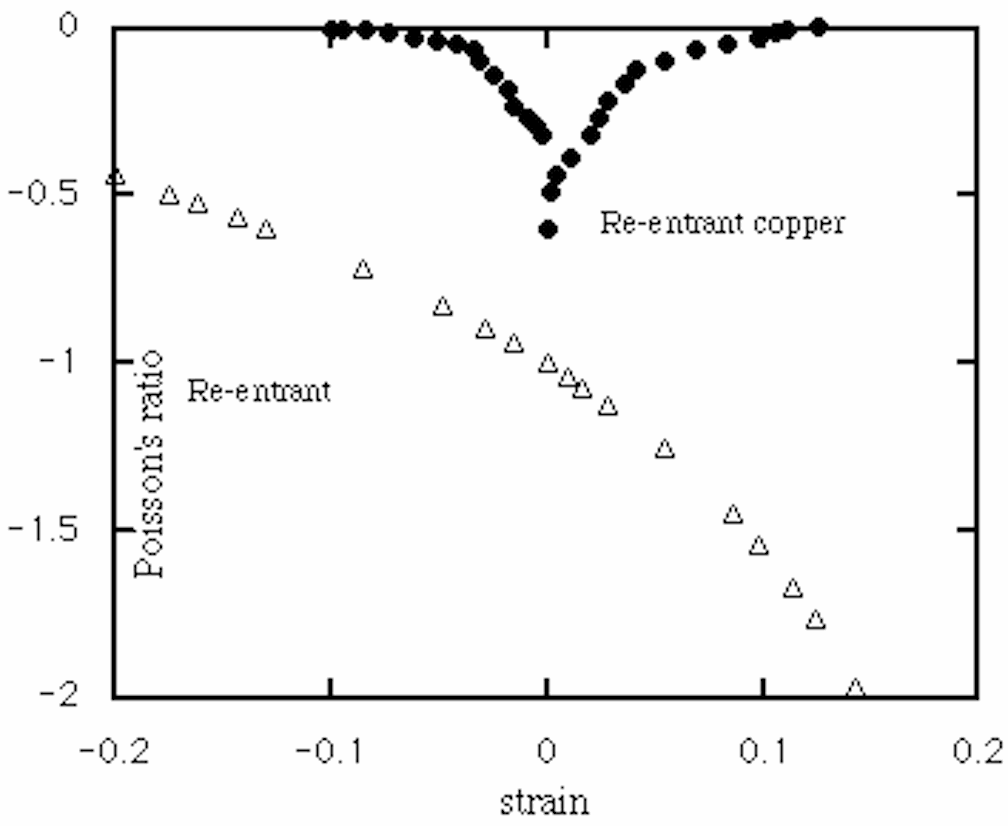
Re-entrant hexagonal honeycomb (theory).
Re -entrant copper foam (experiment).