 Negative Poisson's ratio materials: names- anti-rubber, auxetic, dilational
Negative Poisson's ratio materials: names- anti-rubber, auxetic, dilational

 Names of these materials
Names of these materials
Materials with a negative Poisson's ratio [1] have been called anti-rubber [2], dilational materials [3], or auxetic materials [4] or auxetics. The name anti-rubber arises from the fact that negative Poisson's ratio materials become fatter in cross section when stretched. By contrast rubber becomes thinner. The opposite of auxetic is rubbery. The name dilational arises from the fact that solids with negative Poisson's ratio easily undergo volume changes but resist changes in shape. By contrast, rubbery materials easily undergo shape changes (shear deformation) but are much stiffer in relation to volume changes. The distinction is shown in a map adapted from Milton. The name auxetic, or auxetics after Evans and co-workers (Exeter, U. K.) in a later article and subsequent publications, is derived from the root word for growth, alluding to the lateral expansion which occurs under tension. In that vein, the property of a negative Poisson's ratio can be called auxeticity. More recently, materials in which interesting or extreme properties arise from microstructure rather than composition have been called metamaterials. In many but not all of these, resonant effects in the microstructure are of interest. The name is relatively recent but the concepts and physical examples are not recent. Dynamic resonant effects were reported in the following, accessible on the main Poisson page. Chen, C. P. and Lakes, R. S., "Dynamic wave dispersion and loss properties of conventional and negative Poisson's ratio polymeric cellular materials", Cellular Polymers, 8(5), 343-359 (1989). The word metamaterial was not used at that time. The phrase architected material was not used at that time. Other neologisms have appeared in recent years.
 Description
Description
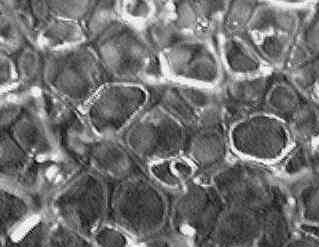
Novel materials are presented, which exhibit a negative Poisson's ratio. Such a material expands laterally when stretched, in contrast to ordinary materials. The original negative Poisson's ratio foam was developed by Rod Lakes.
Foam materials with a negative Poisson's ratio as small as -0.7 were developed [1] in which an inverted or re-entrant cell structure was achieved by isotropic permanent volumetric compression of a conventional foam, resulting in microbuckling of the cell ribs.
The cause of the negative Poisson's ratio in these materials is non-affine deformation.
 In an advance [5], conceptual laminate structures have been presented by Milton. These hierarchical laminates give rise to intentional negative Poisson's ratios combined with mechanical isotropy in two dimensions or in three dimensions [3]. These laminates have structure on several levels of scale; they are hierarchical. By appropriate choice of constituent properties one can achieve Poisson's ratios approaching the lower limit of -1. The laminate Poisson's ratio is close to the rigorous lower bound which is independent of the microstructure, therefore it will not be possible to find microstructures with much lower Poisson's ratio for given constituent stiffnesses.
In an advance [5], conceptual laminate structures have been presented by Milton. These hierarchical laminates give rise to intentional negative Poisson's ratios combined with mechanical isotropy in two dimensions or in three dimensions [3]. These laminates have structure on several levels of scale; they are hierarchical. By appropriate choice of constituent properties one can achieve Poisson's ratios approaching the lower limit of -1. The laminate Poisson's ratio is close to the rigorous lower bound which is independent of the microstructure, therefore it will not be possible to find microstructures with much lower Poisson's ratio for given constituent stiffnesses.
Review articles on auxetic materials, auxetics, anti-rubber, or dilational materials are given by Lakes in [5] and by Evans and Alderson in [6]; more recently, [7], [8].
 References
References
[1] R. S. Lakes, "Foam structures with a negative Poisson's ratio", Science , 235 1038-1040, 1987
[2] J. Glieck, The New York Times, 14 April 1987.
[3] G. Milton, "Composite materials with Poisson's ratios close to -1", J. Mech. Phys. Solids, 40, 1105-1137, 1992
[4] B. D. Caddock, and K. E. Evans, "Microporous materials with negative Poisson's ratio: I. Microstructure and mechanical properties", J. Phys. D., Appl. Phys. , 22, 1877-1882, 1989.
[5] R. S. Lakes, "
Advances in negative Poisson's ratio materials", Advanced Materials (Weinheim, Germany), 5, 293-296, 1993.
[6] K. E. Evans and A. Alderson, "Auxetic materials: functional materials and structures from lateral thinking", Advanced Materials (Weinheim, Germany), 12, 617-628, 2000.
[7] Greaves, G. N., Greer, A. L., Lakes, R. S., and Rouxel, T., "Poisson's Ratio and Modern Materials", Nature Materials, 10, 823-837 Nov. (2011).
In comparing a material's resistance to distort under mechanical load rather than alter in volume, Poisson's ratio offers the fundamental metric by which to compare the performance of any material when strained elastically. The numerical limits are set by 1/2 and -1, between which all stable isotropic materials are found. With new experiments, computational methods and routes to materials synthesis, we assess what Poisson's ratio means in the contemporary understanding of the mechanical characteristics of modern materials. Central to these recent advances, we emphasize the significance of relationships outside the elastic limit between Poisson's ratio and densification, connectivity, ductility and the toughness of solids; and their association with the dynamic properties of the liquids from which they were condensed and into which they melt.
[8] Lakes, R. S., "Negative-Poisson's-Ratio Materials: Auxetic Solids", Annual Review of Materials Research, 47: 63-81 July (2017).
Poisson's ratio had long been considered to be an intrinsic material property, confined within a narrow domain and governed solely by the geometry of interatomic bonds. Materials with designed heterogeneity allow control over the Poisson's ratio. Poisson's ratios of any value within the thermodynamically admissible domain may be attained, including negative Poisson's ratio (called auxetic). In this article, we discuss the role of Poisson's ratio in elasticity, two-dimensional and three dimensional materials, phase transformations, underlying causes in the microstructure and other negative physical properties.
These contain more recent review on auxetic materials / auxetics.
More references are given in the following, and even more in the link to work by others below.
K. W. Wojciechowski, 'Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional systems of hard cyclic hexamers', Molecular Physics 61, 1247-125 (1987).
K. W. Wojciechowski and A. C. Branka, 'Negative Poisson ratio in a two-dimensional "isotropic" model', Physical Review A40, 7222-7225 (1989).
Bowick, M., Cacciuto, A., Thorleifsson, G. , and Travesset, A., "Universal negative Poisson ratio of self-avoiding fixed-connectivity membranes", Phys. Rev. Lett.87, 148103, (2001).
A. Alderson and K. E. Evans, "Molecular origin of auxetic behavior in tetrahedral framework silicates", Phys. Rev. Lett.89, 225503, (2002).

![]() Names of these materials
Names of these materials![]() Description
Description ![]() In an advance [5], conceptual laminate structures have been presented by Milton. These hierarchical laminates give rise to intentional negative Poisson's ratios combined with mechanical isotropy in two dimensions or in three dimensions [3]. These laminates have structure on several levels of scale; they are hierarchical. By appropriate choice of constituent properties one can achieve Poisson's ratios approaching the lower limit of -1. The laminate Poisson's ratio is close to the rigorous lower bound which is independent of the microstructure, therefore it will not be possible to find microstructures with much lower Poisson's ratio for given constituent stiffnesses.
In an advance [5], conceptual laminate structures have been presented by Milton. These hierarchical laminates give rise to intentional negative Poisson's ratios combined with mechanical isotropy in two dimensions or in three dimensions [3]. These laminates have structure on several levels of scale; they are hierarchical. By appropriate choice of constituent properties one can achieve Poisson's ratios approaching the lower limit of -1. The laminate Poisson's ratio is close to the rigorous lower bound which is independent of the microstructure, therefore it will not be possible to find microstructures with much lower Poisson's ratio for given constituent stiffnesses.