Extreme composite materials with negative stiffness inclusions
Preamble
By incorporating constituents of negative stiffness in structures and composites, one can attain extremely high values of mechanical damping, stiffness considered as a viscoelastic modulus, of thermal expansion, or of other physical properties. Negative stiffness is of itself usually unstable but can be stabilized by incorporation in heterogeneous structures or composites. Negative stiffness is associated with buckling on a macroscopic scale or on an interatomic scale associated with phase transformations. Extreme properties via stored energy in the material or in the structure are achieved. We did not call these metamaterials or architected materials; the parlance has since become popular. Similarly, we did not call these active materials; the parlance has since become popular.
Articles
Lakes, R. S., "Extreme damping in compliant composites with a negative stiffness phase"
Philosophical Magazine Letters, 81, 95-100 (2001).
Compliant composite unit cells were made with negative stiffness constituents. Flexible silicone rubber tubes were incorporated in a post-buckled condition to achieve tunable negative stiffness. Large peaks in mechanical damping tan delta were observed in these systems. Maximum damping was orders of magnitude in excess of the material damping of the silicone rubber.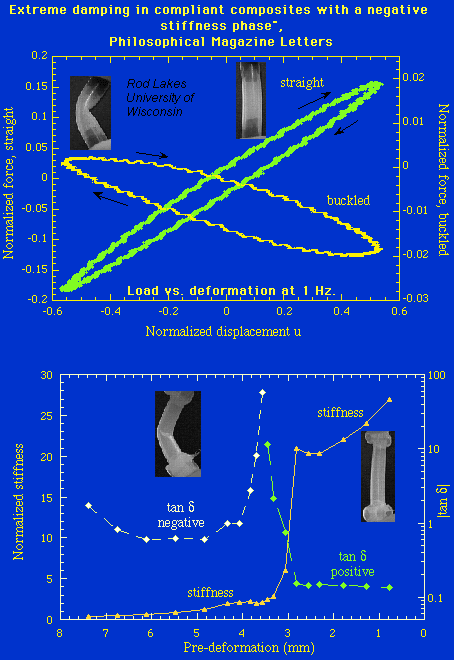 
Download pdf from
Phil. Mag. Letters, or from
here.
Negative Phase delta. Theory diagram: Reuss composite unit cell with negative stiffness phase.
Lakes, R. S., "Extreme damping in composite materials with a negative stiffness phase",
Physical Review Letters 86, 2897-2900, 26 March (2001).
Composites with negative stiffness inclusions in a viscoelastic matrix are shown (theoretically) to have higher stiffness and mechanical damping tan delta than that of either constituent and exceeding conventional Hashin-Shtrikman bounds. The causal mechanism is a greater deformation in and near the inclusions than the composite as a whole. Though a block of negative stiffness (negative modulus) is unstable, negative stiffness inclusions in a composite can be stabilized by the surrounding matrix. Such inclusions may be made from single domains of ferroelastic material below its phase transition temperature or from pre-buckled lumped elements.
Download pdf from
Physical Review Letters, or from
here.
Lakes, R. S., Lee, T., Bersie, A., and Wang, Y. C., "Extreme damping in composite materials with negative stiffness inclusions",
Nature, 410, 565-567, 29 March (2001).
The force applied to deform an elastic object is in the same direction as the displacement: positive stiffness. The force direction is opposite for negative stiffness, possible if there is stored energy or a power source. Negative stiffness is not illegal; usually only unstable. Negative stiffness (negative modulus) differs from negative Poisson's ratio in which lateral expansion occurs upon stretching. Inclusions of negative stiffness can be stabilized in a composite by the surrounding matrix. Experimentally, composites were prepared with a dilute concentration of ferroelastic inclusions in a positive stiffness matrix to stabilize them. In a ferroelastic the free energy in the Landau theory has a relative maximum, corresponding to unstable equilibrium, below its transformation temperature Tc . The composites exhibited large peaks in mechanical damping (tan delta), and large anomalies in stiffness, in harmony with composite theory predictions. The inclusions are more effective than diamond in increasing the composite stiffness at selected temperatures. The underlying physical process is interplay between the positive and negative stiffness phases so that the inclusions deform more than the composite as a whole, giving rise to high local strains. Such composites may be useful as high performance damping materials, as stiff structural elements, or in actuators.
Composites with inclusions of negative stiffness may be called exterlibral since they are on the boundary of balance, or archidynamic since they are based on initial force. They are pertinent to any heterogeneous material in which one constituent undergoes a phase transformation and another does not; also to some materials with a pre-strained constituent. Such composites may be of use as high-performance damping materials, since the figure of merit in the present results exceeds that of commonly used materials (E tan delta less than 0.6 GPa) by a factor of more than twenty. For that purpose, sensitivity to temperature could be reduced via matching inclusion and matrix stiffness.
Bounds on properties of complex heterogeneous materials are generally derived assuming positive phase properties. These bounds can be exceeded if negative stiffness is allowed, permitting extreme properties not previously anticipated. Since in thermoelastic and piezoelectric materials, elasticity is coupled with temperature and electric field respectively, these composites may find use in high performance sensors and actuators.
Experiment diagram. Composite with negative stiffness inclusions. Experimental torsional compliance and mechanical damping tan delta vs. temperature. Open triangles, a composite containing 1 % by volume vanadium dioxide particles in a tin matrix. Points, pure tin for which the damping tan delta = 0.019 over the temperature range considered. Measurements were conducted at 100 Hz, well below resonance, during slow cooling through the ferroelastic phase transition of the inclusions.
Download pdf from
Nature or from
here.
Wang, Y. C. and Lakes, R. S., "Extreme thermal expansion, piezoelectricity, and other coupled field properties in composites with a negative stiffness phase", Journal of Applied Physics, 90, 6458-6465, Dec. (2001).
Particulate composites with negative stiffness inclusions in a viscoelastic matrix are shown to have higher thermal expansion than that of either constituent and exceeding conventional bounds. It is also shown theoretically that other extreme linear coupled field properties including piezoelectricity and pyroelectricity occur in layer- and fiber-type piezoelectric composites, due to negative inclusion stiffness effects. The causal mechanism is a greater deformation in and near the inclusions than the composite as a whole. A block of negative stiffness material is unstable, but negative stiffness inclusions in a composite can be stabilized by the surrounding matrix and can give rise to extreme viscoelastic effects in lumped and distributed composites. In contrast to prior proposed composites with unbounded thermal expansion, neither the assumptions of void spaces nor slip interfaces are required in the present analysis.
link,
pdf.
Rosakis, P., Ruina, A., and Lakes, R. S., "Microbuckling instability in elastomeric cellular solids",
J. Materials Science, 28, 4667-4672 (1993).
Compressive properties of elastic cellular solids are studied via experiments upon foam and upon single cell models. Open cell foam exhibits a monotonic stress-strain relation with a plateau region; deformation is localized in transverse bands. Single cell models exhibit a force-deformation relation which is not monotonic. In view of recent concepts of the continuum theory of elasticity, the banding instability of the foam in compression is considered to be a consequence of the non-monotonic relation between force and deformation of the single cell. The non-monotonic relation entails negative stiffness of the cell over a range of strain.
Download preprint pdf reprint pdf
The negative stiffness represents an instability that can be viewed as a phase transition. Such instability occurs in foams as well as in fiber networks.
Lakes, R. S. and Drugan, W. J., "Dramatically stiffer elastic composite materials due to a negative stiffness phase?",
J. Mechanics and Physics of Solids, 50, 979-1009 (2002).
Composite materials of extremely high stiffness can be produced by employing one phase of negative stiffness. Negative stiffness entails a reversal of the usual codirectional relationship between force and displacement in deformed objects. Negative stiffness structures and materials are possible, but unstable by themselves. We argue here that composites made with a small volume fraction of negative-stiffness inclusions can be stable and can have overall stiffness far higher than that of either constituent. This high composite stiffness is demonstrated via several exact solutions within linearized and also fully nonlinear elasticity, and via the overall modulus tensor estimate of a variational principle valid in this case. We provide an initial discussion of stability, and adduce experimental results which show extreme composite behavior in selected viscoelastic systems under subresonant sinusoidal load. Viscoelasticity is known to expand the space of stability in some cases. We have not yet proved that purely elastic composite materials of the types proposed and analyzed in this paper will be stable under static load. The concept of negative stiffness inclusions is buttressed by recent experimental studies illustrating related phenomena within the elasticity and viscoelasticity contexts. Download pdf.
Wang, Y. C. and Lakes, R. S., "Extreme stiffness systems due to negative stiffness elements", American J. of Physics, 72, Jan. (2004).
When an elastic object is pressed, we expect it to resist by exerting a restoring force. A reversal of this force corresponds to negative stiffness. If we combine elements with positive and negative stiffness in a composite, it is possible to achieve stiffness greater than (or less than) that of any of the constituents. This behavior violates established bounds that tacitly assume that each phase has positive stiffness. Extreme composite behavior has been experimentally demonstrated in a lumped system using a buckled tube to achieve negative stiffness and in a composite material in the vicinity of a phase transformation of one of the constituents. In the context of a composite system, extreme refers to a physical property greater than either constituent. We consider a simple spring model with pre-load to achieve negative stiffness. When suitably tuned to balance positive and negative stiffness, the system shows a critical equilibrium point giving rise to extreme overall stiffness. A stability analysis of a viscous damped system containing negative stiffness springs reveals that the system is stable when tuned for high compliance, but metastable when tuned for high stiffness. The metastability of the extreme system is analogous to that of diamond. The frequency response of the viscous damped system shows that the overall stiffness increases with frequency and goes to infinity when one constituent has a suitable negative stiffness.
Download pdf
Wang, Y. C., Ludwigson, M., and Lakes, R. S., "Deformation of extreme viscoelastic metals and composites", Materials Science and Engineering A, 370, 41-49, April (2004).
The figure of merit for structural damping and damping layer applications is the product of stiffness E and damping tan δ. For most materials, even practical polymer damping layers, E tan δ is less than 0.6 GPa. We consider several methods to achieve high values of this figure of merit: high damping metals, metal matrix composites and composites containing constituents of negative stiffness.
Download pdf
Wang, Y. C. and Lakes, R. S., "Stable extremely-high-damping discrete viscoelastic systems due to negative stiffness elements", Applied Physics Letters, 84, 4451-4453 (2004).
Systems with negative stiffness constituents can have extreme material properties greatly exceeding those of either constituent. We show that a discrete system with a viscoelastic damping element and a negative stiffness element can be made with overall viscoelastic damping orders of magnitude higher than that of any constituent, or of the system with all elements of positive stiffness. The product of stiffness and damping, important for vibration damping, is also enhanced by orders of magnitude. We show this system is unconditionally stable in the high damping regime. The singularity in damping can be made arbitrarily close to the stability boundary.
Download pdf from
aip or
here
Wang, Y. C. and Lakes, R. S., "Stability of negative stiffness viscoelastic systems" , Quarterly of Applied Math., 63, 34-55, March (2005).
We analytically investigate the stability of a discrete viscoelastic system with negative stiffness elements both in the time and frequency domain. Parametric analysis was performed by tuning both the amount of negative stiffness in a standard linear solid, and driving frequency. Stability conditions were derived from the analytical solutions of the differential governing equations and the Lyapunov stability theorem. High frequency response of the system is studied. Stability of singularities in the dissipation tan delta is discussed. It was found that stable singular tan delta is achievable. The system with extreme high stiffness analyzed here was metastable. We established an explicit link for the divergent rates of the metastable system between the solutions of differential governing equations in the time domain and the Lyapunov theorem.
get pdf
Wang, Y. C. and Lakes, R. S., "Negative stiffness induced extreme viscoelastic mechanical properties: stability and dynamics", Philosophical Magazine, 35, 3785-3801, Dec. (2004).
Use of negative stiffness inclusions allows one to exceed the classic bounds upon overall mechanical properties of composite materials. We here analyse discrete viscoelastic 'spring' systems with negative stiffness elements to demonstrate the origin of extreme properties, and analyse the stability and dynamics of the systems. Two different models are analysed: one requires geometrical nonlinear analysis with pre-load as a negative stiffness source and the other is a linearised model with a direct application of negative stiffness. Material linearity is assumed for both models. The metastability is controlled by a viscous element. In the stable regime, extreme high mechanical damping tan delta can be obtained at low frequency. In the metastable regime, singular resonance-like responses occur in tan delta. The pre-stressed viscoelastic system is stable at the equilibrium point with maximal overall compliance and is metastable when tuned for maximal overall stiffness. A reversal in the relationship between the magnitude of complex modulus and frequency is also observed. The experimental observability of the singularities in tan delta is discussed in the context of designed composites and polycrystalline solids with metastable grain boundaries.
Download get pdf
Jaglinski, T. and Lakes, R. S., "Anelastic instability in composites with negative stiffness inclusions", Philosophical Magazine Letters, 84, (12) 803 - 810, Dec. (2004). Composites with VO2 particulate inclusions as a negative stiffness phase were fabricated through powder metallurgy. The composites are predicted to exhibit enhanced anelastic damping by virtue of the partially constrained negative stiffness of the inclusions in the vicinity of a ferroelastic phase transformation, and are predicted to become unstable for sufficiently high concentration (5 volume percent) of inclusions. Composite specimens with 5 volume percent inclusions studied in subresonant dynamic torsion displayed various manifestations of mechanical instability during cooling in a temperature range including the inclusion transformation temperature. Instability was manifested as macroscopic specimen undulations (slow thrashing) and fluctuation of the damping tan delta. Material instability occurs at high inclusion volume fraction in harmony with predictions from composite theory.
Download pdf
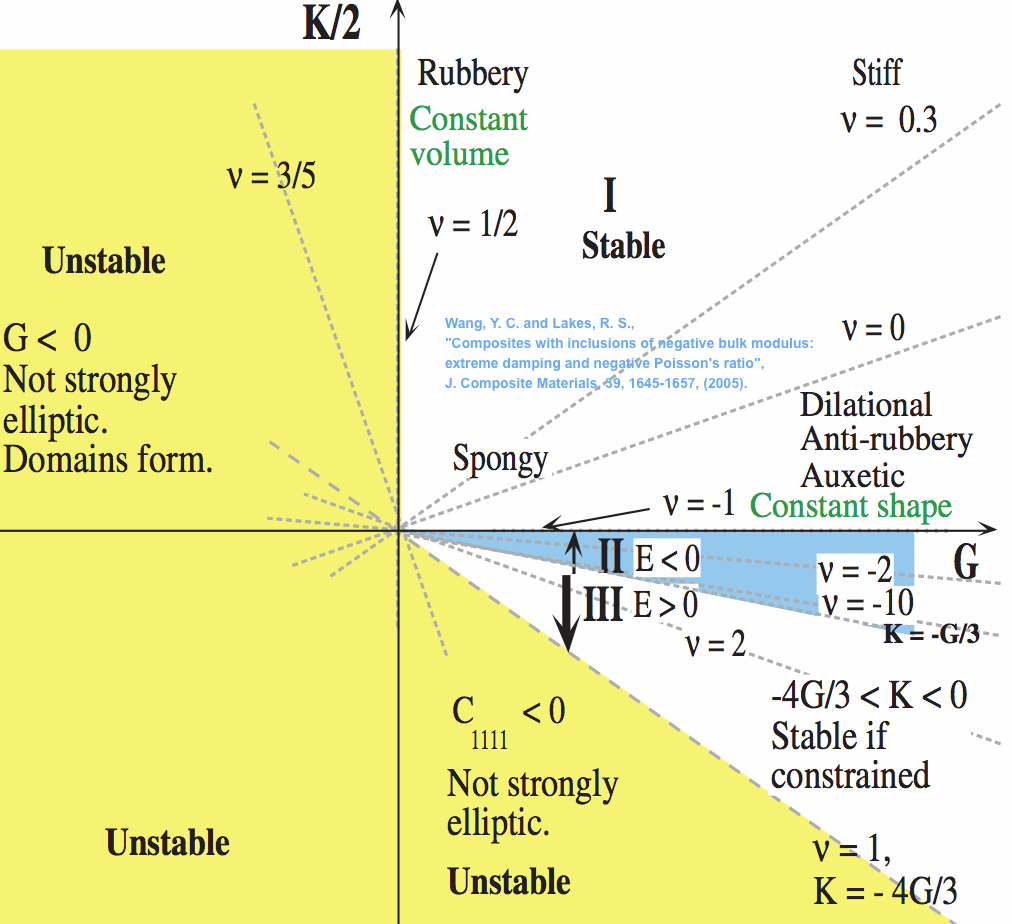
Wang, Y. C. and Lakes, R. S., "Composites with inclusions of negative bulk modulus: extreme damping and negative Poisson's ratio", J. Composite Materials, 39, 1645-1657, (2005). The bulk modulus is the inverse of the compressibility. Negative compressibility has different stability criteria than negative shear modulus considered earlier.
The effect of a negative bulk modulus phase in elastic composites is studied. Negative bulk modulus K is shown to be possible in selected unit cells. In isotropic solids, negative bulk modulus can be attained when negative Poisson's ratio is sufficiently small, below the stability limit (for stress control) Poisson's ratio = -1. Such materials, if used as inclusions, are predicted to be stable with respect to the band formation, even if they are large. Composites with spherical inclusions of negative bulk moduli are shown to exhibit negative Poisson's ratio and anomalies in composite bulk modulus and Young's modulus (and in the corresponding mechanical damping) but not in the shear modulus.
get pdf
Jaglinski, T. Stone, D., and Lakes, R. S., "Internal friction study of a composite with a negative stiffness constituent", J. Mater. Research 20 (9), 2523-2533, Sept. (2005). Composites with negative stiffness constituents can exhibit material properties that exceed conventional bounds. Composites with VO2 as negative stiffness inclusions and tin as the stabilizing matrix were prepared via powder metallurgy. Specimens were tested over a range of temperature in torsion using broadband viscoelastic spectroscopy. Composites processed via powder metallurgy exhibited internal friction anomalies over a broad range of temperatures, in contrast to the single, sharp anomalies reported previously from cast specimens. The detailed material behavior encompassed a variety of responses, which were also dependent on the number of thermal cycles. Composite theory predictions assuming a distribution of negative shear moduli can account for peak broadening.
pdf
Wang, Y. C. and Lakes, R. S., "Two-dimensional viscoelastic discrete triangular system with negative-stiffness components", Philosophical Magazine Letters, 86, 99-112, (2006).
Potential applications of high-damping and high-stiffness composites have motivated extensive research on the effects of negative stiffness inclusions on the overall properties of composites. Recent theoretical advances have been based on the Hashin Shtrikman composite models, one-dimensional discrete viscoelastic systems and a two-dimensional nested triangular viscoelastic network. In this paper, we further analyze the two-dimensional triangular structure containing pre-selected negative-stiffness components to study its underlying deformation mechanisms and stability. Major new findings are structure-deformation evolution with respect to the magnitude of negative stiffness under shear loading and the phenomena related to dissipation induced destabilization and inertia induced stabilization, according to Lyapunov stability analysis. The evolution shows strong correlations between stiffness anomalies and deformation modes. Our stability results reveal that stable damping peaks, i.e. stably extreme effective damping properties, are achievable under hydrostatic loading when the inertia is greater than a critical value. Moreover, destabilization induced by elemental damping is observed with the critical inertia. Regardless of elemental damping, when the
inertia is less than the critical value, a weaker system instability is identified.
pdf.
Jaglinski, T., Frascone , P., Moore, B., Stone, D., and Lakes, R. S., "Internal friction due to negative stiffness in the indium-thallium martensitic phase transformation", Philosophical Magazine, 86, (27 / 21) 4285 - 4303, September (2006).
Internal friction and dynamic shear modulus in an indium-21 atomic percent thallium alloy were measured as functions of frequency and cooling rate using broadband viscoelastic spectroscopy during the martensitic transformation which in this material occurs around 50oC. Microstructural evolution of martensitic bands was captured using time-lapse optical microscopy. The amplitude of damping peaks due to the temperature induced transformation in the polycrystalline alloy were found to exceed those reported by others for single crystals of similar alloy compositions in contrast to the usual reduction in damping in polycrystals. The high temperature portion of the damping peak occurs before martensitic bands are observed, therefore this portion cannot be due to interfacial motion. Constrained negative stiffness of the grains can account for this damping, as well as for amplification of internal friction peaks in these polycrystals and for sigmoid shaped anomalies in the shear modulus at high cooling rates. Surface features associated with a previously unreported pre-martensitic phenomenon are seen at temperatures above martensite-start.
pdf
Moore, B., Jaglinski, T., Stone, D. S., and Lakes, R. S., "Negative incremental bulk modulus in foams", Philosophical Magazine Letters, 86, 651-659, (2006). Negative compressibility is observed in foams under volumetric constraint. Pre-strain is applied. Negative incremental stiffness is known to occur in structures such as post-buckled flexible tubes and single cell models. A single foam cell under uniaxial loading buckles and exhibits a non-monotonic S-shaped deformation curve, which is indicative of negative incremental stiffness. Negative stiffness is not observed in materials, due to instability. For example, individual foam cells display negative stiffness but foams tested in uniaxial compression exhibit a plateau in the stress-strain curve because the buckled cells localise in bands. This behaviour is consistent with the continuum view in which strong ellipticity, hence positive shear modulus G and positive C11 modulus, are required for stability, even for a constrained object. It is hypothesised that a solid with negative bulk modulus can be stabilised by control of surface displacement. Experimentally, foams were hydrostatically compressed under control of volumetric deformation. Negative incremental bulk modulus was observed in foam with 0.4 mm cell size beyond about 20 percent volumetric strain. Foam with large cells 2.5 mm to 4 mm was anisotropic and did not exhibit the cell buckling required for negative modulus.
get pdf.
Jaglinski, T. M., Lakes, R. S., Negative stiffness and negative Poisson's ratio in materials which undergo a phase transformation, in Adaptive Structures: Engineering Applications, edited by D. Wagg, I. Bond, P. Weaver, M. Friswell, J. Wiley, Chichester, England, ch. 8, p. 231-246, (2007).
get pdf.
Wang, Y. C., Swadener, J. G. and Lakes, R. S., "Anomalies in stiffness and damping of a 2D discrete viscoelastic system due to negative stiffness components", Thin Solid Films, 515, 3171-3178, (2007). get pdf
Shang, X. and Lakes, R. S., "Stability of elastic material with negative stiffness and negative Poisson's ratio", Physica Status Solidi (b), 244, 1008-1026 (2007). Cover article. Stability of cuboids and cylinders of an isotropic elastic material with negative stiffness under partial constraint is analyzed using an integral method and Rayleigh quotient. It is not necessary that the material exhibit a positive definite strain energy to be stable. The elastic object under partial constraint may have a negative bulk modulus K and yet be stable. A cylinder of arbitrary cross section with the lateral surface constrained and top and bottom planar surfaces is stable provided the shear modulus G > 0 and -G/3 < K < 0 or K > 0.
get pdf.
Jaglinski, T., Kochmann, D., Stone, D., Lakes, R. S., Materials with viscoelastic stiffness greater than diamond, Science 315, 620-622, Feb. 2 (2007)
go-link. We show that composite materials can exhibit a viscoelastic (Young's) modulus far higher than that of either constituent. The modulus (but not strength) was observed to be substantially greater than that of diamond. These composites contain barium titanate inclusions, which undergo a volume change phase transformation if not constrained. In the composite the inclusions are partially constrained by the surrounding metal matrix. The constraint stabilizes the negative bulk modulus (inverse compressibility) of inclusions. The composites are stiffer than diamond over a narrow temperature range.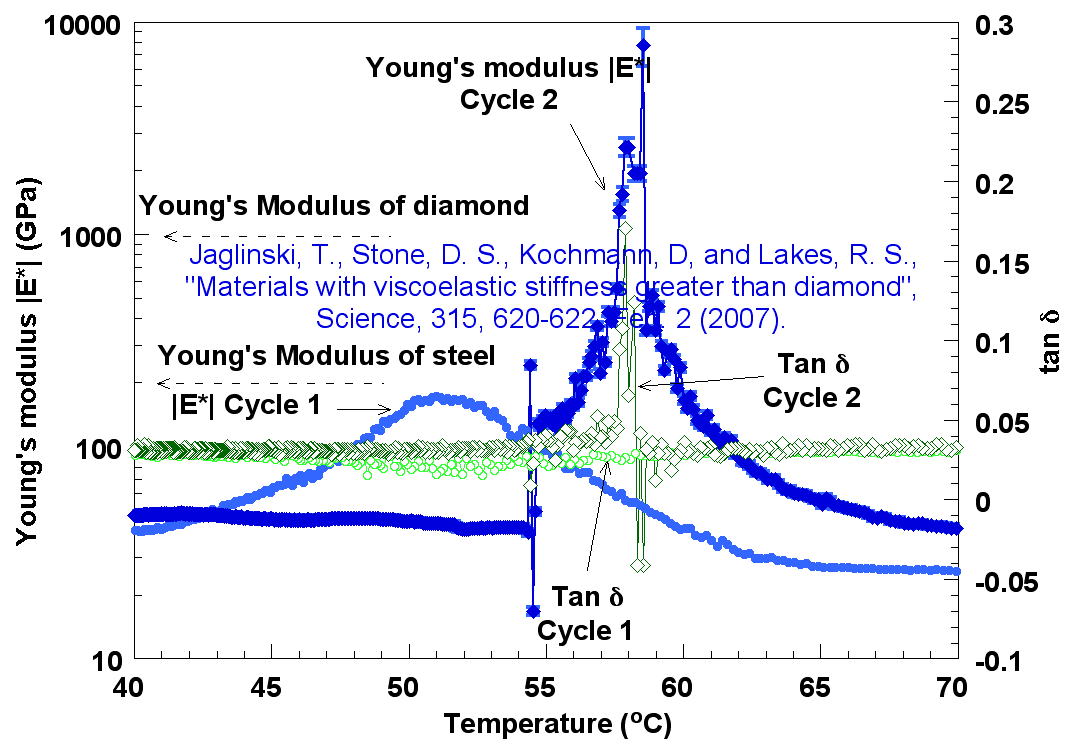 
Carpick, R., Yap, H, Lakes, R. S., "Mechanical instabilities of individual multi-walled carbon nanotubes under cyclic axial compression", Nano Letters, 7(5); 1149-1154 (2007).
get pdf
Yap, H, Lakes, R. S., Carpick, R., "Negative stiffness and enhanced damping of individual multiwalled nanotubes", Phys. Rev. B, 77, 045423 (2008).
get pdf
Lakes, R., Wojciechowski, K. W., "Negative compressibility, negative Poisson's ratio, and stability", Physica Status Solidi, 245, No. 3, 545-551, Feb 4 (2008). Negative compressibility does not violate any physical law. Arguments within thermodynamics that suggest impossibility of negative compressibility actually contain an assumption of a positive definite strain energy. That assumption does not account for materials with initial stress under a constraint.
get pdf
Dong, L., Stone, D. S., and Lakes, R. S., "Broadband viscoelastic spectroscopy measurement of mechanical loss and modulus of polycrystalline BaTiO3 vs. temperature and frequency", Phys. Stat. Sol. (b), 245, 2422-2432, Nov. (2008). Characterization of pure polycrystalline BaTiO3 was carried out by means of Broadband Viscoelastic Spectroscopy (BVS) and Differential Scanning Calorimetry (DSC) above ambient temperature. A peak in mechanical loss has been observed near the Curie point 130 deg. C. The magnitude of the peak increases with thermal rate and decreases with frequency. Expressions for the peak magnitude have been derived based upon available models describing the first order phase transition. Mechanical anomalies were observed outside the vicinity of the phase transition. Transition temperature measured by BVS differed from that via DSC; the effect of stress on the ferroelastic transformation is a possible cause. Isothermal frequency scans revealed a hump in mechanical loss in the vicinity of the transition temperature below 1 Hz and a modulus decrease with decreasing frequency. Quasi isothermal studies revealed a significant softening in bulk modulus and a transient negative Poisson's ratio during the tetragonal to cubic phase transition.
get pdf
Dong, L. Stone, D. S., Lakes, R. S., "Softening of bulk modulus and negative Poisson's ratio in barium titanate ceramic near the Curie point", Philosophical Magazine Lett. 90, 23-33, Jan. (2010). Formal journal formatted reprints are available; if you want one, please request it. Get informal pdf.
Substantial softening in the bulk modulus (a factor of five) and a negative Poisson ratio (-0.25) have been observed via broadband viscoelastic spectroscopy in the vicinity of the Curie point of a barium titanate ceramic. These effects were observed under electrical short-circuit conditions at low deformation frequencies. Softening was less in an electric open circuit or at higher frequencies. Softening of individual elastic modulus tensor elements is known to occur near phase transformations, but softening of the bulk modulus has not previously been well reported.
See also piezoelectric materials
Dong, L., Stone, D. S., and Lakes, R. S., "Sharp low frequency dissipative effects in tetragonal BaTiO3 ceramics,"J. Appl. Physics 107, 023514, (2010). get pdf.
Copyright American Institute of Physics AIP link.
Mechanical anomalies damping peaks sharper than Debye peaks, in contrast to a broad relaxation peak were observed in tetragonal barium titanate ceramic via broadband viscoelastic spectroscopy at low frequencies 10 Hz at ambient temperature after aging at 90 degrees C for 15 h. The sharp peaks disappear after aging above the Curie point 150 degrees C for 10 h. Mechanical anomalies are tentatively attributed to negative stiffness heterogeneity.
Dong, L., Stone, D. S., and Lakes, R. S., "Anelastic anomalies and negative Poisson's ratio in tetragonal BaTiO3 ceramics", Applied Phys. Lett. 96, 141904 (2010). Anelastic anomalies, sharp variations in modulus and damping with temperature, were observed in tetragonal BaTiO3 via broadband viscoelastic spectroscopy after aging at 50 deg C for 15 h. The effect was most pronounced under electrical short circuit condition, at low frequency and under small excitation strain 10-6. Softening in bulk modulus and negative Poisson's ratio were observed near 60 deg C. Effects are attributed to an oxygen vacancy mechanism. A relaxational model cannot account for sharp response at smaller strains. Heterogeneity of negative stiffness is considered as a cause.
Applied Physics Letters link. get pdf.
Dong, L., Stone, D. S., and Lakes, R. S., "Dielectric and viscoelastic properties of KNbO3 doped BaTiO3", J. Appl. Phys., 109, 063531 (2011). Fine grain (1-2 micron) 2%, 3% KNbO3-BaTiO3 ceramics have been synthesized via the solid state reaction method. Fine and coarse grain ceramics sintered at different temperatures exhibit peaks in dielectric constant and internal friction in the vicinity of transition temperatures. Doping lowered the Curie point and raised the temperatures for the structural transformations between orthorhombic and rhombohedral symmetry and broadened the response near the transformations. Dielectric and viscoelastic responses sharpened with increasing sintering cycles. This effect is attributed to a reduced core-shell effect. Doped ceramic exhibited a relaxation peak due to oxygen vacancy with a similar activation energy and relaxation time as pure material. The steep increase in dielectric constant and internal friction in the ferroelectric phase and the reduced dielectric and mechanical anomaly in the vicinity of the transformations in the fine grain ceramics are attributed to the internal stress built up at the grain boundaries. Other possible mechanisms involved such as oxygen vacancy pinning effect, constrained negative stiffness 90 deg. domain bands and the liquid phase effect have also been discussed.
get pdf,
Journal link, this issue,
Journal link, contents.
See also piezoelectric materials
Dong, L., Stone, D. S., and Lakes, R. S., "Viscoelastic sigmoid anomalies in BaZrO3-BaTiO3 near phase transformations due to negative stiffness heterogeneity", Journal of Materials Research, 26,(11), 1446-1452 (2011). BaZrO3-BaTiO3 ceramics exhibit a shift in transformation temperatures as revealed by dielectric and viscoelastic spectroscopy; a phase diagram has been established. Sigmoid anomalies in Poisson's ratio and bulk modulus during the ferroelastic transitions were observed in doped materials, which are not predicted by standard theories for phase transformations. Hashin-Shtrikman composite model with negative stiffness heterogeneity can well explain this phenomenon. Negative stiffness heterogeneity is considered to be caused by the strained BaTiO3 unit cells in the vicinity of BaZrO3 rich zones under the perturbation of lattice reconstruction.
get pdf.
Journal cover pdf.
Journal link, JMR
Lakes, R. S., "Stable singular or negative stiffness systems in the presence of energy flux", Philosophical Magazine Letters, 92, 226-234, (2012). We report stable systems which exhibit quasistatic stiffness that can be negative or tend to infinity without external constraint. They are based on coupled fields in the non-equilibrium presence of energy flux that is modulated by force. They evade thermodynamic restrictions by relaxing a restrictive assumption: equilibrium. Negative values of physical properties, including compressibility and heat capacity, are considered forbidden in classical thermodynamics; such analyses provide bounds on the stiffness and other properties of multiphase materials. Stable negative and singular stiffness is demonstrated experimentally in a piezoelectric system and in a thermoelastic granular material. Stiffness is tunable from negative stiffness to large positive stiffness. Coupled fields occur naturally under a wide range of conditions and form the basis for many forms of technology including sensors, actuators, and electric coolers. Because all materials exhibit at least one coupled field effect, the concept is broadly general and is applicable to attaining extreme values of any physical property e.g. stiffness, permittivity, piezoelectricity.
get pdf
We developed high performance structural dampers based on negative stiffness.
Dong, L., Stone, D. S., and Lakes, R. S., "Advanced damper with negative structural stiffness elements", Smart materials and structures, 21 07502 (2012). When a flexible flat-ends column is aligned in a post-buckled condition, a negative structural stiffness and large hysteresis (i.e., high damping) can be achieved provided the ends of the column undergo tilting from flat to edge contact. Stable axial dampers with initial modulus equivalent to that of the parent material and with enhanced damping were designed and built using constrained negative stiffness effects entailed by post-buckled press-fit flat-ends columns. get pdf.
Jaglinski, T. M. and Lakes, R. S., "Zn-Al based metal matrix composites with high stiffness and high viscoelastic damping" Journal of Composite Materials, 46: 755-763, April (2012)
A maximal product of stiffness and viscoelastic damping (E tan delta), a figure of merit for damping layers, is desirable for structural damping applications. Particulate-reinforced metal matrix composites were prepared by ultrasonic agitation of the melt and composed of the zinc aluminum (ZnAl) alloy Zn80Al20 (in wt%) as the lossy matrix and SiC or BaTiO3 as the particulate reinforcements. ZnAl-SiC composites were stiffer and exhibited higher damping at acoustic frequencies in comparison to the base alloy. ZnAl-SiC composites were superior to Sn-SiC composites and possessed an E tan delta in excess of 0.6 GPa, the maximum figure of merit provided by commercial polymer damping layers. Furthermore, ZnAl-SiC composites displayed a high figure of merit over a broad temperature range. ZnAl-BaTiO3 composites exhibited anomalies in modulus and damping associated with partial restraint of the phase transformation; one specimen was much stiffer than diamond over a narrow temperature range.
get pdf
Lakes, R. S., "Giant enhancement in effective piezoelectric sensitivity by pyroelectric coupling", EPL (Europhysics Letters), 98, 47001 May (2012).
We report stable two layer composites that exhibit large enhancement of effective piezoelectric sensitivity to more than 20,000 pC/N in the presence of a thermal gradient. They are based on coupled fields in the non-equilibrium presence of energy flux that is modulated by force. Thermal flux is modulated by a granular contact layer so that electric polarization of pyroelectric origin contributes to stress generated electric polarization. Effective piezoelectric sensitivity is enhanced by at least two orders of magnitude and is higher than that of known commercial and research materials. The result illustrates the potential of relaxing the usual assumption of equilibrium in the presence of coupled field to attain extremely high effective properties.
Get preprint pdf
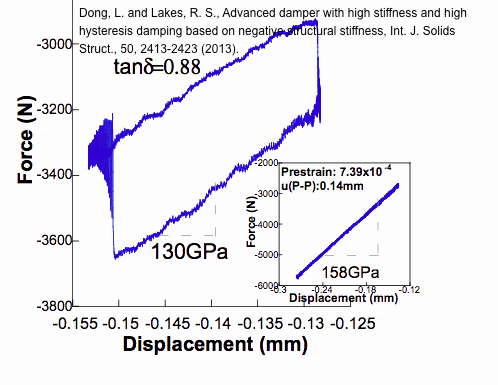Dong, L. and Lakes, R. S., Advanced damper with high stiffness and high hysteresis damping based on negative structural stiffness, Int. J. Solids Struct., 50, 2413-2423 (2013). High structural damping combined with high stiffness is achieved by negative stiffness elements. Negative incremental structural stiffness occurs when a column with flat ends is subjected to snap-through buckling. Large hysteresis (i.e., high damping) can be achieved provided the ends of the column undergo tilting from flat to edge contact. The column configuration provides high structural stiffness. Stable axial dampers with initial modulus similar to that of the parent material and with enhanced damping were designed built and tested. Effective damping of approximately two and stiffness-damping product of approximately 200 GPa were achieved in such dampers consisting of stainless steel columns. This is a significant improvement for this figure of merit (i.e., the stiffness-damping product), which generally cannot exceed 0.6 GPa for currently used damping systems. get pdf
Kalathur, H., Lakes, R. S., Column dampers with negative stiffness: high damping at small amplitude, Smart Materials and structures, 22, 084013 (8pp) (2013). High structural damping combined with high initial stiffness is achieved at small amplitude via negative stiffness elements. These elements consist of columns in the vicinity of the post-buckling transition between contact of flat surfaces and edges of the ends for which negative incremental structural stiffness occurs. The column configuration provides a high initial structural stiffness equal to the intrinsic stiffness of the column material. Columns of the polymers polymethyl methacrylate (PMMA) and polycarbonate were used. By tuning the pre-strain, a very high mechanical damping was achieved for small amplitude oscillations. The product of effective stiffness and effective damping as a figure of merit |E tan delta effective of about 1.5 GPa was achieved for polymer column dampers in the linear domain and about 1.62 GPa in the small amplitude nonlinear domain. For most materials this value generally never exceeds 0.6 GPa.
journal link. get preprint pdf
H. Kalathur, T. M. Hoang, R. S. Lakes and W. J. Drugan, "Buckling Mode Jump at Very Close Load Values in Unattached Flat-End Columns: Theory and Experiment", J. Appl. Mech. 81(4), 041010 Sept. (2013).
Buckling of compressed flat-end columns loaded by unattached flat platens is shown, theoretically and experimentally, to occur first at the critical load and associated mode shape of a built-in column, followed extremely closely by a second critical load and different mode shape characterized by column end-tilt. The theoretical critical load for secondary or end tilt buckling is shown to be only 0.13% greater than the critical load for primary buckling, in which the ends are in full contact with the compression platens. The experimental value is consistent with this theoretical one. Interestingly, under displacement control, the first buckling instability is characterized by a smoothly-increasing applied load, whereas the closely-following second instability causes an abrupt and large load drop (and hence exhibits incremental negative stiffness). The end tilt buckling gives rise to large hysteresis that can be useful in structural damping but that is non-conservative and potentially catastrophic in the context of design of structural support columns. get pdf
Kalathur, H. and Lakes, R. S., "Enhancement in piezoelectric sensitivity via negative structural stiffness" Journal of Intelligent Material Systems and Structures, 27(18) 2568-2573 (2016).
Effective piezoelectric sensitivity of bimorph strip actuators was enhanced by negative structural stiffness. Negative stiffness was achieved in brass strips post-buckled in compression to an 'S' shape; the brass strip was placed in series with the bimorph. The negative stiffness was tuned by adjusting the brass strip length. The effective piezoelectric sensitivity in units of displacement per volt input, increased as the inverse of the overall stiffness of the series element. The maximum observed enhancement in effective piezoelectric sensitivity was at least a factor of six, at 1 Hz in comparison to the value when no negative stiffness was used. This corresponds to a maximum effective sensitivity of about 36 microns/V in comparison to the baseline effective sensitivity of about 6.1 microns/V, at 1 Hz. The value is several orders of magnitude (almost 40,000 times) higher than the typical value of sensitivity for the material comprising the individual bimorph strip actuator.
DOI: 10.1177/1045389X15624802
journal link get preprint pdf
Balch, S. and Lakes, R. S., "Amelioration of waves and micro-vibrations by micro-buckling in open celled foam", Cellular Polymers, 36, 1-11, Feb. (2017). Open cell polymer foam exhibits both an intrinsic micro-vibration frequency and a cut off frequency associated with resonance of the cell ribs. Compression of the foam causes regions of local buckling of ribs. Incipient buckling gives rise to negative stiffness and enhanced amelioration of waves. Transmitted wave amplitude is reduced by compression below and near the cut off frequency. preprint pdf
Balch, S. and Lakes, R. S., "Lumped negative stiffness damper for absorption of flexural waves in a rod", Smart Materials and Structures, 26 045022 (6pp) (2017)
A damper based on negative stiffness from column tilt buckling was used to achieve enhanced mechanical damping of bending vibration of a rod. Damping increased by a factor of three, via a damper column that was only about 0.2% of the mass of the aluminum alloy rod to be damped.
journal doi link
preprint pdf
Ha, C. S., Plesha, M. E., Lakes, R. S., "Design, Fabrication, and Analysis of Lattice Exhibiting Energy Absorption via Snap-through Behavior", Materials and Design, 254, 426-437 (2018).
In this study, an energy absorption lattice, comprised of multiple tetra beam plate unit cells with negative stiffness, was designed, fabricated by selective laser sintering method, and analyzed both numerically and experimentally. Snap-through behavior of the unit cell developed due to negative stiffness caused by geometric nonlinearity from large deflection of the constituent elastic beams, resulting in energy absorption. A criterion for the unit cell to achieve the snap through behavior was investigated numerically in terms of the beam slenderness ratio and the inclined angle. This approach was chosen to facilitate control of energy dissipation performance and further design space such as tuning force threshold. The unit cell with the selected geometric parameters was then created and used to construct the energy absorption lattice. Load displacement relationships of the lattices obtained from cyclic loading tests disclosed an area enclosed by two distinct loading and unloading curves, which indicates energy dissipation. This was shown both numerically and experimentally. Drop tests were also performed to investigate energy loss of the lattices due to an impact. An energy absorption phenomenon was revealed by observing a reduced rebound height when the lattice exhibited the snap-through behavior.
journal link
C. S. Ha, R. S. Lakes, M. E. Plesha, Cubic negative stiffness lattice structure for energy absorption: numerical and experimental studies, International Journal of Solids and Structures, vol. 178-179, P. 127-135, 1 December (2019).
We present a new type of a truly three dimensional cubic negative stiffness lattice structure that can achieve energy absorption and recover its original configuration under cyclic loading in excess of a strain of approximately 20%. This structure was composed of multiple unit cells exploiting negative stiffness from controlled elastic buckling. Structural properties were designed to be tuned by adjusting geometry. The effective Poisson's ratio was equal to zero regardless of the constituent material. Geometric parameters that can lead to the desired energy absorption without yielding the structure were determined by finite element analysis. We then fabricated samples representing the lattice structure with different sizes through additive manufacturing and performed cyclic loading experiments to capture stress strain hysteresis loops. Results clearly showed that the designed structure was capable of absorbing mechanical energy effectively with a full recovery of geometry in three principal directions and that the amount of energy absorbed during cyclic loading increases with its size.
doi journal link
Lakes, R. S., "Stability of Cosserat solids: size effects, ellipticity and waves", Journal of mechanics of materials and structures (JoMMS), 13 (1) 83-91 (2018).
We consider stability in Cosserat solids. To obtain restrictions on elastic constants based on positive definite strain energy, energy terms are tacitly assumed to be independent. In finite-size objects, however, the terms are linked in Cosserat materials. Therefore, in contrast to classical solids, the stability of Cosserat solids appears to depend on the size and shape of the specimen, provided strong ellipticity is satisfied. Stability in the presence of stored energy is possible. Solids with microstructure and stored energy offer the potential to facilitate attainment of extreme behavior in the presence of spatial gradients. Snap- through buckling in torsion is envisaged by analogy to the axial buckling concept used for composites with negative stiffness inclusions. It is possible to support compressive load in a stable manner but to dissipate energy in the presence of spatial gradients as in torsion or bending.
journal link
preprint pdf
DOI: 10.2140/jomms.2018.13.83
We also obtain experimental results on stability of Cosserat solids in relation to warp.
R. S. Lakes, Softening of Cosserat sensitivity in a foam: warp effects, International Journal of Mechanical Sciences, Volume 192, 106125, 15 February 2021.
Buckling gives rise to softening of the structural stiffness of columns; buckling of ribs gives rise to softening of the incremental elastic modulus of foams. Softening of Cosserat characteristic lengths occurs in pre compressed foam material as determined from warp of cross sections of a square bar in torsion. Warp in the foam is reduced considerably in comparison with the predictions of classical elasticity. Pre compression increases the warp in comparison with the warp observed without pre compression. The effect is attributed to release of energy stored via pre compression.
https://doi.org/10.1016/j.ijmecsci.2020.106125
preprint pdf
Further lattices exhibiting negative stiffness snap through are in progress.
The negative stiffness dampers based on our original negative stiffness concepts at top (2001) have been built upon, scaled up and used for applications. See this link.
Related papers provide analyses of stability.
W. J. Drugan, "Elastic composite materials having a negative stiffness can be stable" Physical Review Letters 98, 055502, (2007).
get pdf
W. J. Drugan, Wave propagation effects possible in solid composite materials by use of stabilized negative-stiffness components, Journal of the Mechanics and Physics of Solids, Volume 136, March (2020), 103700
doi link
The following article discloses regions of negative stiffness in polymers via molecular modeling.
Yoshimoto, K., Jain, T. S., Van Workum, K., Nealey, P. F., de Pablo, J. J., "Mechanical heterogeneities in model polymer glasses at small length scales", Physical Review Letters 93(17):175501, October 18, (2004).
Related research.
Drugan, W. J. "Two Exact Micromechanics-Based Nonlocal Constitutive Equations for Random Linear Elastic Composite Materials," Journal of the Mechanics and Physics of Solids, 51, 1745-1772, (2003).
A Hashin-Shtrikman-Willis variational principle is employed to derive two exact micromechanics based nonlocal constitutive equations relating ensemble averages of stress and strain for two-phase and also many types of multi-phase random linear elastic composite materials. Download pdf.
Other systems and materials that entail use of a power source include those that are describable by odd elasticity and those that are describable by non-Hermitian operators.
Demonstrations
Snap through. Illustration of instability.
Ring deformation.
Illustration of Reuss model stabilized by displacement control by the hand of the demonstrator. The ring has positive stiffness and the pre-buckled column has negative stiffness. Observe how the ring deforms. First it deforms in compression as it is pressed indicating positive stiffness of the column. As the column is deformed into an S shape, the ring deforms in tension as it is pressed, showing the reversal of force associated with the negative structural stiffness of the column, so negative stiffness in the transverse direction.
Blurbs
Physics Focus Blurb
Nature Physics Portal Research Highlights
Blurb
See also other publicity.
We thank the National Science Foundation, DARPA, and ARO for sponsorship of some this research.
If you are interested in commercial applications, please contact the Wisconsin Alumni Research Foundation (WARF) for information on US and international patents and licensing.
For current research reports,
log in.
This site is copyright, 2002 - 2024, Rod Lakes. All rights reserved.
Research by others
Follow-on research with advanced dampers may use key words such as force amplification, geometrical amplification, lattices with snap through elements, leaf springs, structural logic, material logic, structural logic unit. The subject is becoming increasingly popular. Many people call these metamaterials.
A related topic in reversal physics, negative refraction, References
This was originally suggested by V. G. Veselago, "The electrodynamics of substances with simultaneously negative values of e and m", Sov. Phys. Uspekhi 10, 509-514 (1968).
Nicorovici, N. A. and Milton, G. W., "On the cloaking effects associated with anomalous localized resonance", Proceedings of the Royal Society of London, A, 462, 3027 - 3059 (2006).
journal link
G. M. Gehring, A. Schweinsberg, C. Barsi, N. Kostinski, and R. W. Boyd "Observation of Backward Pulse Propagation Through a Medium with a Negative Group Velocity" Science 12 May 2006: 895-897.
A. N. Grigorenko, A. K. Geim, H. F. Gleeson, Y. Zhang, A. A. Firsov, I. Y. Khrushchev and J. Petrovic, "Nanofabricated media with negative permeability at visible frequencies," Nature 438, 335-338, 17 Nov. (2005).
N. Fang, H. Lee, C. Sun, X. Zhang, "Sub diffraction limited optical imaging with a silver superlens" Science 308: 534-537, (2005).
J. B. Pendry, "A Chiral Route to Negative Refraction" Science, 306: 1353-1355, (2004).
A. A. Houck, J. B. Brock, and I. L. Chuang, "Experimental Observations of a Left-Handed Material That Obeys Snell's Law", Phys. Rev. Lett. 90, 137401 (2003).
R. A. Shelby, D. R. Smith, and S. Schultz, "Experimental Verification of a Negative Index of Refraction" Science 292, 77 (2001).
J. B. Pendry, "Negative Refraction Makes a Perfect Lens" Phys. Rev. Lett. 85, 3966 (2000).
M. Notomi, "Theory of light propagation in strongly modulated photonic crystals: Refractionlike behavior in the vicinity of the photonic band gap" Phys. Rev. B 62, 10 696 (2000).
M. C. K. Wiltshire, J. B. Pendry, I. R. Young, D. J. Larkman, D. J. Gilderdale, and J. V. Hajnal, "Microstructured Magnetic Materials for RF Flux Guides in Magnetic Resonance Imaging" Science 291, 849 (2001).
R. J. Blaikie and S. J. McNab, Microelectron. Eng. 61-2, 97 (2002).
V. G. Veselago, Sov. Phys. Usp. 10, 509 (1968).
R. A. Shelby, D. R. Smith, S. C. Nemat-Nasser, and S. Schultz, "Microwave transmission through a two-dimensional, isotropic, left-handed metamaterial" Appl. Phys. Lett. 78, 489 (2000).
P. M. Valanju, R. M. Walser, and A. P. Valanju, "Wave Refraction in Negative-Index Media: Always Positive and Very Inhomogeneous" Phys. Rev. Lett. 88, 187401 (2002).
N. Garcia and M. Nieto-Verperinas, Opt. Lett. 27, 885 (2002).
N. Garcia and M. Nieto-Verperinas, "Left-Handed Materials Do Not Make a Perfect Lens" Phys. Rev. Lett. 88, 207403 (2002).
D. R. Smith, S. Schultz, P. Markos, and C. M. Soukoulis, Phys. Rev. B 65, 195103 (2002).
J. B. Pendry, A. J. Holden, W. J. Stewart, and I. Youngs, "Extremely Low Frequency Plasmons in Metallic Mesostructures" Phys. Rev. Lett. 76, 4773 (1996).
D. R. Smith, W. J. Padilla, D. C. Vier, S. C. Nemat-Nasser, and S. Schultz, "Composite Medium with Simultaneously Negative Permeability and Permittivity" Phys. Rev. Lett. 84, 4184 (2000).
Nicorovici, N. A. Mcphedran, R. C., Milton, G. W., "Optical and dielectric properties of partially resonant systems." Phys. Rev. B 49: 8479-8482. (1994).
R. W. Ziolkowski and E. Heyman, "Wave propagation in media having negative permittivity and permeability" Phys. Rev. E 64, 056625 (2001).
Negative capacitance, as with negative stiffness, is unstable in isolation. Negative capacitance has been studied in the context of phase transitions in ferroelectrics and with reduction of power requirements in microelectronics.
Biological solids such as those in the ear have a metabolic source of power. Damping and stiffness can be negative.
T. Gold, Hearing. II. The physical basis of the action of the cochlea, Proceedings of the Royal Society of London. Series B, Biological Sciences, 135, 492-498, (1948).
P. Martin, A. D. Mehta, and A. J. Hudspeth, Negative hair-bundle stiffness betrays a mechanism for mechanical amplification by the hair cell, PNAS 97 (22) 12026-1203 (2000).
A. J. Hudspeth, Integrating the active process of hair cells with cochlear function, Nature Reviews Neuroscience 15, 600?614 (2014).
Top